题目内容
1.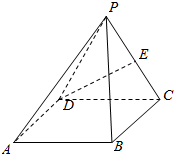 如图,四棱锥P-ABCD中,底面四边形ABCD是正方形,侧面PDC是边长为a的正三角形,且平面PDC⊥底面ABCD,E为PC的中点.
如图,四棱锥P-ABCD中,底面四边形ABCD是正方形,侧面PDC是边长为a的正三角形,且平面PDC⊥底面ABCD,E为PC的中点.(1)求异面直线PA与DE所成的角的余弦值;
(2)求点D到面PAB的距离.
分析 (1)连结AC,BD交于点O,连结EO.由四边形ABCD为正方形,且AO=CO,PE=EC,可得PA∥EO,从而得到∠DEO为异面直线PA与DE所成的角,然后通过求解直角三角形求解;
(2)取DC的中点M,AB的中点N,连PM、MN、PN,由线面平行的判断得到DC∥面PAB,可得D到面PAB的距离等于点M到面PAB的距离,过M作MH⊥PN于H,由线面垂直的性质可得PM⊥DC,进一步得到PM⊥面ABCD,即PM⊥AB,然后推得MH⊥面PAB,则MH就是点D到面PAB的距离,然后求解直角三角形得答案.
解答  解(1)连结AC,BD交于点O,连结EO.
解(1)连结AC,BD交于点O,连结EO.
∵四边形ABCD为正方形,∴AO=CO,又∵PE=EC,∴PA∥EO,
∴∠DEO为异面直线PA与DE所成的角,
∵面PCD⊥面ABCD,AD⊥CD,∴AD⊥面PCD,∴AD⊥PD.
在Rt△PAD中,PD=AD=a,则PA=$\sqrt{2}a$,
∴$EO=\frac{1}{2}PA=\frac{\sqrt{2}}{2}a$,
又∵DE=$\frac{\sqrt{3}}{2},DO=\frac{\sqrt{2}}{2}a$,
∴$cos∠DEO=\frac{\frac{3}{4}{a}^{2}+\frac{1}{2}{a}^{2}-\frac{1}{2}{a}^{2}}{2×\frac{\sqrt{3}}{2}a×\frac{\sqrt{2}}{2}a}=\frac{\sqrt{6}}{4}$;
(2)取DC的中点M,AB的中点N,连PM、MN、PN.
∵DC∥AB,DC?面PAB,∴DC∥面PAB,
∴D到面PAB的距离等于点M到面PAB的距离.
过M作MH⊥PN于H,
∵面PDC⊥面ABCD,PM⊥DC,
∴PM⊥面ABCD,∴PM⊥AB,
又∵AB⊥MN,PM∩MN=M,
∴AB⊥面PMN.∴面PAB⊥面PMN,
∴MH⊥面PAB,
则MH就是点D到面PAB的距离.
在Rt△PMN中,MN=a,PM=$\frac{\sqrt{3}}{2}a$,
∴$PN=\sqrt{{a}^{2}+(\frac{\sqrt{3}}{2}a)^{2}}=\frac{\sqrt{7}}{2}a$,
∴$MH=\frac{MN•PM}{PN}=\frac{a•\frac{\sqrt{3}}{2}a}{\frac{\sqrt{7}}{2}a}=\frac{\sqrt{21}a}{7}$.
点评 本题考查空间异面直线所成角,考查了线面角,考查空间想象能力和计算能力,是中档题.

 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案| A. | 1 | B. | $\frac{3}{5}$ | C. | $\frac{1}{3}$ | D. | 0 |
| A. | 与a,b都相交 | B. | 与a,b都垂直 | C. | 与a平行,与b垂直 | D. | 与a,b都平行 |
| A. | P(B)=$\frac{2}{5}$ | |
| B. | 事件B与事件A1相互独立 | |
| C. | P(B|A1)=$\frac{5}{11}$ | |
| D. | P(B)的值不能确定,它与A1,A2,A3中哪一个发生都有关 |
| A. | 1 | B. | 2 | C. | $\sqrt{5}$ | D. | $2\sqrt{5}$ |