题目内容
已知函数f(x)的图象是连续不断的,有如下x,f(x)对应表:函数f(x)在区间[1,6]上零点至少有
( )
| x | 1 | 2 | 3 | 4 | 5 | 6 |
| f(x) | 36.14 | 15.55 | -3.92 | 10.88 | -52.49 | -32.06 |
| A、2个 | B、3个 | C、4个 | D、5个 |
考点:函数零点的判定定理
专题:函数的性质及应用
分析:函数f(x)的图象是连续不断的在(a,b),f(a)•f(b)<0,
函数f(x)在(a,b)上至少有1个零点,根据表格函数值判断即可.
函数f(x)在(a,b)上至少有1个零点,根据表格函数值判断即可.
解答:
解:根据表格得出:函数f(x)的图象是连续不断的在(a,b),
f(a)•f(b)<0,
∴函数f(x)在(a,b)上至少有1个零点,
∵f(2)•f(3)<0,f(3)•f(4)<0,f(4)•f(5)<0,
∴函数f(x)在区间[2,5]上零点至少有3个零点
∴函数f(x)在区间[1,6]上零点至少有 3个零点
故选:B
f(a)•f(b)<0,
∴函数f(x)在(a,b)上至少有1个零点,
∵f(2)•f(3)<0,f(3)•f(4)<0,f(4)•f(5)<0,
∴函数f(x)在区间[2,5]上零点至少有3个零点
∴函数f(x)在区间[1,6]上零点至少有 3个零点
故选:B
点评:本题考查了函数的表格表示方法,函数零点的判定定理,属于容易题.

练习册系列答案
相关题目
若函数f(x)唯一的一个零点同时在(0,8),(4,8),(6,8)内,则下列结论正确的是( )
| A、函数f(x)在区间(7,8)内有零点 |
| B、函数f(x)在区间(6,7)或(7,8)内有零点 |
| C、函数f(x)在区间(0,7)内无零点 |
| D、函数f(x)在区间(0,6]上无零点 |
 已知三棱柱ABC-A1B1C1的侧棱与底面ABC垂直,且AA1=4,AC=BC=2,∠ACB=90°.
已知三棱柱ABC-A1B1C1的侧棱与底面ABC垂直,且AA1=4,AC=BC=2,∠ACB=90°.

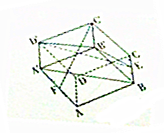 如图,在棱长为2的正方体AC′中,E,F为BC和AA′的中点
如图,在棱长为2的正方体AC′中,E,F为BC和AA′的中点