题目内容
20.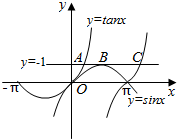 如图,已知A,B,C为直线y=1与函数y=sinx,y=tanx的图象在第一象限的三个相邻交点,若线段AC的长度记为|AC|,则|AB|:|BC|=( )
如图,已知A,B,C为直线y=1与函数y=sinx,y=tanx的图象在第一象限的三个相邻交点,若线段AC的长度记为|AC|,则|AB|:|BC|=( )| A. | 1:2 | B. | 1:3 | C. | 1:4 | D. | 1:5 |
分析 先根据条件求得A、B、C的值,可得|AB|和|BC|的值,从而求得|AB|:|BC|的值.
解答 解:∵A,B,C为直线y=1与函数y=sinx,y=tanx的图象在第一象限的三个相邻交点,
∴tanA=,∴A=$\frac{π}{4}$,点B的坐标为($\frac{π}{2}$,1),且tanC=1,C∈(π,$\frac{3π}{2}$),∴C=$\frac{5π}{4}$.
∴|AB|=$\frac{π}{2}$-$\frac{π}{4}$=$\frac{π}{4}$,|BC|=$\frac{5π}{4}$-$\frac{π}{2}$=$\frac{3π}{4}$,∴|AB|:|BC|=1:3,
故选:B.
点评 本题主要考查特殊角的三角函数的值,把线段的长度之比化为横坐标的差之比,属于基础题.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
11.函数$y={x^2}+\frac{1}{x}+1$在x=1处的切线方程是( )
| A. | x-y+2=0 | B. | x-y-4=0 | C. | x+y-4=0 | D. | x+y+2=0 |
8.若角α=2rad(rad为弧度制单位),则下列说法错误的是( )
| A. | 角α为第二象限角 | B. | α=$\frac{360°}{π}$ | C. | sinα>0 | D. | sinα<cosα |
5.用更相减损术法,计算56和264的最大公约数时,需要做的减法次数是( )
| A. | 5、 | B. | 6 | C. | 7 | D. | 8 |
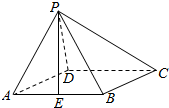 如图,在四棱锥P-ABCD中,底面ABCD是菱形,PA=PB,且侧面PAB⊥平面ABCD,点E是AB的中点.
如图,在四棱锥P-ABCD中,底面ABCD是菱形,PA=PB,且侧面PAB⊥平面ABCD,点E是AB的中点.