题目内容
10.已知函数$f(x)=\left\{\begin{array}{l}{x^3},x≤0\\ x+\frac{1}{x}-3,x>0\end{array}\right.$,若关于x的方程$f(2x+\frac{1}{2})=m$有3个不同的解,则m的取值范围是(-1,0].分析 关于x的方程$f(2x+\frac{1}{2})=m$有3个不同的解可化为f(x)=m有三个不同的解,从而利用数形结合求解即可.
解答 解:作函数$f(x)=\left\{\begin{array}{l}{x^3},x≤0\\ x+\frac{1}{x}-3,x>0\end{array}\right.$的图象如下,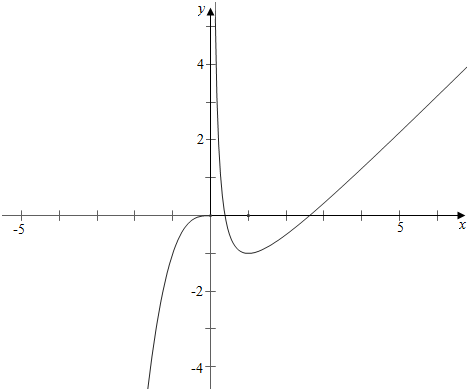 ,
,
令t=2x+$\frac{1}{2}$,易知对每一个t,都有且只有一个x与之对应,
故关于x的方程$f(2x+\frac{1}{2})=m$有3个不同的解可化为f(x)=m有三个不同的解,
结合图象可知,
当-1<m≤0时,$f(x)=\left\{\begin{array}{l}{x^3},x≤0\\ x+\frac{1}{x}-3,x>0\end{array}\right.$与y=m的图象有三个不同的交点,
故答案为(-1,0].
点评 本题考查了转化思想的应用及数形结合的思想应用,同时考查了函数的图象与方程的根的关系应用.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
20.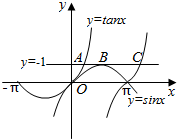 如图,已知A,B,C为直线y=1与函数y=sinx,y=tanx的图象在第一象限的三个相邻交点,若线段AC的长度记为|AC|,则|AB|:|BC|=( )
如图,已知A,B,C为直线y=1与函数y=sinx,y=tanx的图象在第一象限的三个相邻交点,若线段AC的长度记为|AC|,则|AB|:|BC|=( )
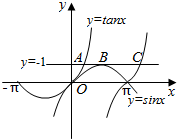 如图,已知A,B,C为直线y=1与函数y=sinx,y=tanx的图象在第一象限的三个相邻交点,若线段AC的长度记为|AC|,则|AB|:|BC|=( )
如图,已知A,B,C为直线y=1与函数y=sinx,y=tanx的图象在第一象限的三个相邻交点,若线段AC的长度记为|AC|,则|AB|:|BC|=( )| A. | 1:2 | B. | 1:3 | C. | 1:4 | D. | 1:5 |
15.某同学在画函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象时,列表如下:
(1)请将上表数据补全,并直接写出函数f(x)的解析式;
(2)将函数f(x)图象上各点的纵坐标不变,横坐标缩短为原来的$\frac{1}{2}$,得到函数y=g(x)的图象,求函数y=g(x)在[0,$\frac{π}{2}$]上的最大值M,最小值N,并求M-N的值.
| x | $\frac{2π}{3}$ | $\frac{5π}{6}$ | |||
| ωx+φ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| Asin(ωx+φ) | 0 | 2 | 0 | -2 |
(2)将函数f(x)图象上各点的纵坐标不变,横坐标缩短为原来的$\frac{1}{2}$,得到函数y=g(x)的图象,求函数y=g(x)在[0,$\frac{π}{2}$]上的最大值M,最小值N,并求M-N的值.
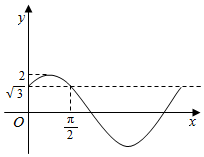 设函数f(x)=Asin(ωx+φ)(A,ω>0,0<|φ|<π)在一个周期内的图象如图所示.
设函数f(x)=Asin(ωx+φ)(A,ω>0,0<|φ|<π)在一个周期内的图象如图所示.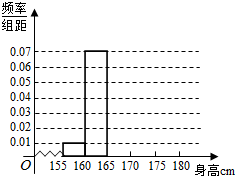 某校为了调查学生身体生长发育情况,随机抽取200名学生测得它们的身高(单位:cm),并按照区间[155,160),[160,165),[165,170),[170,175),[175,180)分组,得到样本的频率分布直方图.由于操作不慎,区间[165,170),[170,175),[175,180)的频率分布直方图被破坏了,如图所示.已知频率分布直方图中[165,170),[170,175),[175,180)间的矩形的高依次成等差数列,并且身高在[170,175)内的人数是身高在[175,180)的人数的2倍.
某校为了调查学生身体生长发育情况,随机抽取200名学生测得它们的身高(单位:cm),并按照区间[155,160),[160,165),[165,170),[170,175),[175,180)分组,得到样本的频率分布直方图.由于操作不慎,区间[165,170),[170,175),[175,180)的频率分布直方图被破坏了,如图所示.已知频率分布直方图中[165,170),[170,175),[175,180)间的矩形的高依次成等差数列,并且身高在[170,175)内的人数是身高在[175,180)的人数的2倍.