题目内容
10.已知函数f(x)=4+loga(x-2),(a>0,且a≠1)其图象过定点P,角α的始边与x轴的正半轴重合,顶点为坐标原点,终边过定点P,则$\frac{sinα+2cosα}{sinα-cosα}$=10.分析 利用对数函数的图象特征,求得点P的坐标,再利用任意角的三角函数的定义,求得tanα的值,再利用同角三角函数的基本关系,求得要求式子的值.
解答 解:∵函数f(x)=4+loga(x-2),(a>0,且a≠1)其图象过定点P(3,4),
角α的始边与x轴的正半轴重合,顶点为坐标原点,终边过定点P,∴x=3,y=4,r=|OP|=5,
∴tanα=$\frac{y}{x}$=$\frac{4}{3}$,则$\frac{sinα+2cosα}{sinα-cosα}$=$\frac{tanα+2}{tanα-1}$=10,
故答案为:10.
点评 本题主要考查对数函数的图象特征,任意角的三角函数的定义,同角三角函数的基本关系,属于基础题.

练习册系列答案
相关题目
18.已知向量$\overrightarrow a=(1,-2)$,向量$\overrightarrow b$满足$|{\overrightarrow b}|=2$,$\overrightarrow a•\overrightarrow b$夹角为$\frac{π}{3}$,则$\overrightarrow a•\overrightarrow b$=( )
| A. | $\sqrt{5}$ | B. | 2 | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
4.已知a>c>1>b>0,则( )
| A. | b-a<b-c | B. | logab>logcb | C. | ab+cb<(a+c)b | D. | loga(c-b)>logc(a-b) |
5.为了了解青少年的肥胖是否与常喝碳酸饮料有关,现对30名青少年进行调查,得到如下列联表:
已知从这30名青少年中随机抽取1名,抽到肥胖青少年的概率为$\frac{4}{15}$.
(1)请将列联表补充完整;(2)是否有99.5%的把握认为青少年的肥胖与常喝碳酸饮料有关?
独立性检验临界值表:
参考公式:${K^2}=\frac{{n{{({ad-bc})}^2}}}{{({a+b})({c+d})({a+c})({b+d})}}$,其中n=a+b+c+d.
| 常 喝 | 不常喝 | 总 计 | |
| 肥 胖 | 2 | ||
| 不肥胖 | 18 | ||
| 总 计 | 30 |
(1)请将列联表补充完整;(2)是否有99.5%的把握认为青少年的肥胖与常喝碳酸饮料有关?
独立性检验临界值表:
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
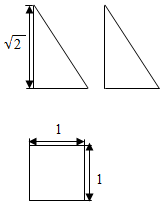 某几何体的三视图如图所示,设该几何体中最长棱所在的直线为m,与直线m不相交的其中一条棱所在直线为n,则直线m与n所成的角为$\frac{π}{3}$.
某几何体的三视图如图所示,设该几何体中最长棱所在的直线为m,与直线m不相交的其中一条棱所在直线为n,则直线m与n所成的角为$\frac{π}{3}$.