题目内容
已知点m是直线l:
x-y+3=0与x轴的交点,将直线l绕点m旋转30°,求所得到的直线l′的方程.
| 3 |
考点:直线的点斜式方程
专题:直线与圆
分析:求出直线l与x轴的交点M的坐标,然后分l顺时针和逆时针旋转求出直线l的倾斜角,再进一步分析斜率的情况,斜率不存在时直接写出直线方程,斜率存在时由直线方程的点斜式求得直线方程.
解答:
解:在方程
x-y+3=0中,取y=0,得x=-
.
∴M(-
,0),
直线
x-y+3=0的斜率为
,则其倾斜角为60°,
直线l绕点M旋转30°,若是逆时针,则直线l′的倾斜角为90°,
∴直线l′的方程为x=-
;
若是顺时针,则直线l′的倾斜角为30°,
∴直线l′的斜率为
,
∴直线l′的方程为y-0=
(x+
),即x-
y+
=0.
| 3 |
| 3 |
∴M(-
| 3 |
直线
| 3 |
| 3 |
直线l绕点M旋转30°,若是逆时针,则直线l′的倾斜角为90°,
∴直线l′的方程为x=-
| 3 |
若是顺时针,则直线l′的倾斜角为30°,
∴直线l′的斜率为
| ||
| 3 |
∴直线l′的方程为y-0=
| ||
| 3 |
| 3 |
| 3 |
| 3 |
点评:本题考查了直线方程的点斜式,考查了直线的倾斜角与斜率的关系,是基础题.

练习册系列答案
相关题目
在等比数列{an}中,a2=2,a5=16,则数列{an}的通项公式为( )
| A、an=2n | ||
| B、an=2n-1 | ||
C、an=(
| ||
D、an=(
|
函数f(x)=Asin(ωx+φ)(A≠0,ω≠0),则f(x) ( )
| A、是非奇函数非偶函数 |
| B、奇偶性与φ有关 |
| C、奇偶性与ω有关 |
| D、奇偶性与A有关 |
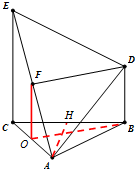 如图,在多面体ECABD中,EC⊥平面ABC,DB∥EC,△ABC为正三角形,F为EA的中点,EC=AC=2,BD=1.
如图,在多面体ECABD中,EC⊥平面ABC,DB∥EC,△ABC为正三角形,F为EA的中点,EC=AC=2,BD=1. 已知三角形△ABC的三个顶点分别为A(-1,0),B(1,0),C(0,1).
已知三角形△ABC的三个顶点分别为A(-1,0),B(1,0),C(0,1).