题目内容
 如图,已知抛物线C:y2=2px(p>0)上的点(
如图,已知抛物线C:y2=2px(p>0)上的点(| 5 |
| 2 |
(1)求抛物线C和圆E的方程;
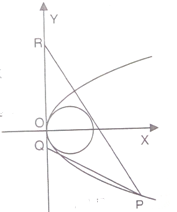
(2)若圆E内切于△PQR,其中Q,R在y轴上,且R点在Q点上方,P在抛物线C上且在x轴下方,当△PQR的面积取最小值时,求直线PR和PQ的方程.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)由抛物线C:y2=2px(p>0)上的点(
,a)到焦点F的距离为3,可得
+
=3,解得p,即可得出抛物线C和圆E的方程;
(2)设P(x0,y0),R(0,y1),Q(0,y2),y1>y2,则直线PR的方程为:y=
x+y1.由直线与圆相切的性质可得:
=1,注意到x0>2,上式化简为(x0-2)
+2y0y1-x0=0,同理可得(x0-2)
+2y0y2-x0=0.因此y1,y2 是方程(x0-2)y2+2y0y-x0=0的两个根,可得|y1-y2|=
.因此S△PQR=
×
×x0=(x0-2)+
+4利用基本不等式的性质即可得出.
| 5 |
| 2 |
| p |
| 2 |
| 5 |
| 2 |
(2)设P(x0,y0),R(0,y1),Q(0,y2),y1>y2,则直线PR的方程为:y=
| y0-y1 |
| x0 |
| |y0-y1+x0y1| | ||||
|
| y | 2 1 |
| y | 2 2 |
| 2x0 |
| x0-2 |
| 1 |
| 2 |
| 2x0 |
| x0-2 |
| 4 |
| x0-2 |
解答:
解:(1)∵抛物线C:y2=2px(p>0)上的点(
,a)到焦点F的距离为3,
∴
+
=3,解得p=1.
∴抛物线C:y2=2x,
圆E:(x-1)2+y2=1.
(2)设P(x0,y0),R(0,y1),Q(0,y2),y1>y2,则直线PR的方程为:y=
x+y1.
由直线与圆相切得:
=1,
注意到x0>2,上式化简为(x0-2)
+2y0y1-x0=0,
同理可得(x0-2)
+2y0y2-x0=0.
∴y1,y2 是方程(x0-2)y2+2y0y-x0=0的两个根,
∴|y1-y2|=
=
.
∴S△PQR=
×
×x0=
=(x0-2)+
+4≥8,当且仅当x0=4时,S△PQR有最小值为8.
此时,P(4,-2
),y1,2=
±2.
∴直线PR的方程是y=
x+
+2.
直线PQ的方程是y=-
x+
-2.
| 5 |
| 2 |

∴
| p |
| 2 |
| 5 |
| 2 |
∴抛物线C:y2=2x,
圆E:(x-1)2+y2=1.
(2)设P(x0,y0),R(0,y1),Q(0,y2),y1>y2,则直线PR的方程为:y=
| y0-y1 |
| x0 |
由直线与圆相切得:
| |y0-y1+x0y1| | ||||
|
注意到x0>2,上式化简为(x0-2)
| y | 2 1 |
同理可得(x0-2)
| y | 2 2 |
∴y1,y2 是方程(x0-2)y2+2y0y-x0=0的两个根,
∴|y1-y2|=
| ||
| x0-2 |
| 2x0 |
| x0-2 |
∴S△PQR=
| 1 |
| 2 |
| 2x0 |
| x0-2 |
| ||
| x0-2 |
| 4 |
| x0-2 |
此时,P(4,-2
| 2 |
| 2 |
∴直线PR的方程是y=
3
| ||
| 4 |
| 2 |
直线PQ的方程是y=-
3
| ||
| 4 |
| 2 |
点评:本题考查了抛物线与圆的标准方程及其性质、直线与圆相切问题转化为方程联立可得根与系数的关系、弦长公式、三角形的面积计算公式、基本不等式的性质,考查了推理能力与计算能力,属于难题.

练习册系列答案
相关题目
下列四个函数:①y=x+1;②y=x-1;③y=x2-1;④y=
,其中定义域与值域相同的是( )
| 1 |
| x |
| A、①②③ | B、①②④ |
| C、②③ | D、②③④ |
若直线l1,l2的方向向量分别为
=(1,2,3),
=(-
,-1,-
),则l1,l2的位置关系是( )
| v1 |
| v2 |
| 1 |
| 2 |
| 3 |
| 2 |
| A、垂直 | B、重合 |
| C、平行 | D、平行或重合 |
平面内过点A(-2,0),且与直线x=2相切的动圆圆心的轨迹方程是( )
| A、y2=-2x |
| B、y2=-4x |
| C、y2=-8x |
| D、y2=-16x |