题目内容
凼数f(x)=loga(2x2+ax+2)没有最小值,则a的集合为 .
考点:函数的最值及其几何意义
专题:综合题,函数的性质及应用
分析:先根据复合函数的单调性确定函数g(x)=2x2+ax+2的单调性,进而分a>1和0<a<1两种情况讨论:①当a>1时,考虑对数函数的图象与性质得到要使y=loga(2x2+ax+2)没有最小值,必须g(x)min≤0;②当0<a<1时g(x)=2x2+ax+2没有最大值,从而使得函数y=loga(2x2+ax+2)没有最小值.最后取这两种情形的并集即可.
解答:
解:令g(x)=2x2+ax+2(a>0,且a≠1),
①当a>1时,y=logax在R+上单调递增,
∴要使y=loga(2x2+ax+2)没有最小值,必须g(x)min≤0,
∴△≥0,
解得a≤-4或a≥4
∴a≥4;
②当0<a<1时,g(x)=2x2+ax+2没有最大值,从而使得函数y=loga(2x2+ax+2)没有最小值,符合题意.
综上所述:0<a<1或a≥4.
故答案为:{a|0<a<1或a≥4}.
①当a>1时,y=logax在R+上单调递增,
∴要使y=loga(2x2+ax+2)没有最小值,必须g(x)min≤0,
∴△≥0,
解得a≤-4或a≥4
∴a≥4;
②当0<a<1时,g(x)=2x2+ax+2没有最大值,从而使得函数y=loga(2x2+ax+2)没有最小值,符合题意.
综上所述:0<a<1或a≥4.
故答案为:{a|0<a<1或a≥4}.
点评:本题考查对数函数的值域最值,着重考查复合函数的单调性,突出分类讨论与转化思想的考查,是中档题.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目
已知向量
=(-3,4),
=(1,m),若
•(
-
)=0,则m=( )
| a |
| b |
| a |
| a |
| b |
A、
| ||
B、-
| ||
| C、7 | ||
| D、-7 |
设数列{an}的前n项和为Sn,且a1=1,{Sn+nan}为常数列,则an=( )
A、
| ||
B、
| ||
C、
| ||
D、
|
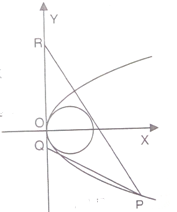 如图,已知抛物线C:y2=2px(p>0)上的点(
如图,已知抛物线C:y2=2px(p>0)上的点(