题目内容
下列四个函数：①y=x+1；②y=x-1；③y=x2-1；④y=
，其中定义域与值域相同的是（ ）
| 1 |
| x |
| A、①②③ | B、①②④ |
| C、②③ | D、②③④ |
考点：函数的值域,函数的定义域及其求法
专题：函数的性质及应用
分析：根据函数解析式分别求解定义域，值域即可判断．
解答：
解：：①y=x+1；定义域R，值域R，
②y=x-1；定义域R，值域R，
③y=x2-1；定义域R，值域（-1，+∞）
④y=
，定义域，（-∞，0）∪（0，+∞），值域：（-∞，0）∪（0，+∞），
∴①②④定义域与值域相同
故选：B
②y=x-1；定义域R，值域R，
③y=x2-1；定义域R，值域（-1，+∞）
④y=
| 1 |
| x |
∴①②④定义域与值域相同
故选：B
点评：本题考查了函数的性质，利用解析式求解定义域，值域，属于中档题，但是难度不大．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
已知f（x）=x2-3x，则f′（0）=（ ）
| A、△x-3 |
| B、（△x）2-3△x |
| C、-3 |
| D、0 |
若对?x∈R，有f（-x）=-f（x），g（-x）=g（x），且x＞0时，有f′（x）＜0，g′（x）＞0，则x＜0时，有（ ）
| A、f′（x）＞0，g′（x）＞0 |
| B、f′（x）＞0，g′（x）＜0 |
| C、f′（x）＜0，g′（x）＞0 |
| D、f′（x）＜0，g′（x）＜0 |
已知向量
=（-3，4），
=（1，m），若
•（
-
）=0，则m=（ ）
| a |
| b |
| a |
| a |
| b |
A、
| ||
B、-
| ||
| C、7 | ||
| D、-7 |
函数f（x）=x2-2tx-4（t∈R）在闭区间[0，1]上的最小值记为g（t）．则g（t）的函数解析式（ ）
A、g（t）=
| ||||||
| B、g（t）=-t2+2 | ||||||
| C、g（t）=-t2+2t | ||||||
| D、g（t）=-t2+2t+2 |
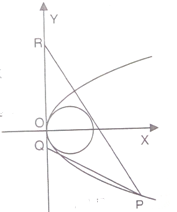如图，已知抛物线C：y2=2px（p＞0）上的点（