题目内容
过双曲线
-y2=1的两焦点作实轴的垂线，分别与渐近线交于A、B、C、D四点．则矩形ABCD的面积为 ．
| x2 |
| 3 |
考点：双曲线的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：求出双曲线的a，b，c，可得焦点坐标和渐近线方程，令x=2，x=-2求得矩形的顶点坐标，求出矩形ABCD的相邻两边长，即可得到所求面积．
解答：
解：双曲线
-y2=1的a=
，b=1，c=
=2，
则双曲线的焦点F1（-2，0），F2（2，0），
渐近线方程为y=±
x，
令x=-2，可得y=±
；令x=2，可得y=±
．
则有A（-2，
），B（-2，-
），C（2，-
），D（2，
），
则矩形ABCD的面积为|AB|•|BC|=
×4=
．
故答案为：
．
| x2 |
| 3 |
| 3 |
| a2+b2 |
则双曲线的焦点F1（-2，0），F2（2，0），
渐近线方程为y=±
| ||
| 3 |
令x=-2，可得y=±
2
| ||
| 3 |
2
| ||
| 3 |
则有A（-2，
2
| ||
| 3 |
2
| ||
| 3 |
2
| ||
| 3 |
2
| ||
| 3 |
则矩形ABCD的面积为|AB|•|BC|=
4
| ||
| 3 |
16
| ||
| 3 |
故答案为：
16
| ||
| 3 |
点评：本题考查双曲线的方程和性质，考查渐近线方程的运用，求出矩形的顶点坐标是解题的关键．
练习册系列答案
相关题目
若对?x∈R，有f（-x）=-f（x），g（-x）=g（x），且x＞0时，有f′（x）＜0，g′（x）＞0，则x＜0时，有（ ）
| A、f′（x）＞0，g′（x）＞0 |
| B、f′（x）＞0，g′（x）＜0 |
| C、f′（x）＜0，g′（x）＞0 |
| D、f′（x）＜0，g′（x）＜0 |
非零向量
，
满足2
•
=
2
2，|
|+|
|=2，则
，
的夹角θ的最小值为（ ）
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知向量
=（-3，4），
=（1，m），若
•（
-
）=0，则m=（ ）
| a |
| b |
| a |
| a |
| b |
A、
| ||
B、-
| ||
| C、7 | ||
| D、-7 |
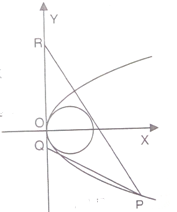如图，已知抛物线C：y2=2px（p＞0）上的点（