题目内容
17.设函数f(x)=ln(x+1)-$\frac{kx}{x+1}$+1(x>-1)(1)讨论f(x)的单调性;
(2)k>0,若f(x)的最小值为g(k),当0<k1<k2且k1+k2=2,比较g(k1)与g(k2)的大小.
分析 (1)求出函数的导数,通过讨论k的范围,求出函数的单调区间即可;
(2)求出f(x)的最小值,求出g(k1)-g(k2)的差,令h(k)=ln$\frac{k}{2-k}$-2k+2,(0<k<1),根据函数的单调性求出h(k)<0,从而比较g(k1)与g(k2)的大小即可.
解答 解:(1)f(x)的定义域为(-1,+∞),
f'(x)=$\frac{1}{x+1}$-$\frac{k}{{(x+1)}^{2}}$=$\frac{x-(k-1)}{{(x+1)}^{2}}$,
令f'(x)>0得:x>k-1,
当k-1≤-1即k≤0时,f(x)的单调递增区间是(-1,+∞);
当k-1>-1即k>0时,f(x)的单调递减区间是(-1,k-1),
f(x)的单调递增区间是(k-1,+∞);
(2)k>0时,由(2)得:
f(x)的单调递减区间是(-1,k-1),
f(x)的单调递增区间是(k-1,+∞);
故f(x)的最小值是f(k-1)=g(k)=lnk-k+2,
当0<k1<k2且k1+k2=2,则k2=2-k1,
故0<k1<1,
g(k1)-g(k2)=lnk1-k1+2-ln(2-k1)+2-k1-2=ln$\frac{{k}_{1}}{2{-k}_{1}}$-2k1+2,
令h(k)=ln$\frac{k}{2-k}$-2k+2,(0<k<1),
h′(k)=$\frac{{2(k-1)}^{2}}{k(2-k)}$>0,
故h(k)在(0,1)递增,
故h(k)<h(1)=0,
故h(k1)<h(k2).
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及分类讨论思想,是一道中档题.

练习册系列答案
相关题目
8.已知函数 f ( x) 的部分图象如图所示,则 f ( x) 的解析式可以是( )
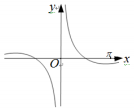

| A. | f(x)=$\frac{{2-{x^2}}}{2x}$ | B. | f(x)=$\frac{cosx}{x^2}$ | C. | f(x)=$\frac{{{{cos}^2}x}}{x}$ | D. | f(x)=$\frac{cosx}{x}$ |
12.平行四边形ABCD的两条对角线相交于点M,点P是线段BD上任意一点.若$|\overrightarrow{AB}|=2,|\overrightarrow{AD}|=1$,且∠BAD=60°,则$\overrightarrow{AP}•\overrightarrow{CP}$的取值范围是( )
| A. | $[1,\frac{7}{4}]$ | B. | $[-\frac{7}{4},-1]$ | C. | $[-\sqrt{2},-1]$ | D. | $[-1,\sqrt{2}]$ |
2.已知集合A={x|x2-2x<0},B={y|y=|x|+1,x∈R},则A∩∁RB=( )
| A. | (0,2) | B. | [1,2) | C. | (0,1] | D. | (0,1) |
9.执行如图所示的程序框图,则输出的结果是( )


| A. | $\frac{1}{6}$ | B. | $\frac{5}{6}$ | C. | $\frac{1}{7}$ | D. | $\frac{6}{7}$ |
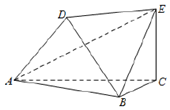 如图,以A、B、C、D、E为顶点的六面体中,△ABC和△ABD均为等边三角形,且平面ABC⊥平面ABD,EC⊥平面ABC,EC=$\sqrt{3}$,AB=2.
如图,以A、B、C、D、E为顶点的六面体中,△ABC和△ABD均为等边三角形,且平面ABC⊥平面ABD,EC⊥平面ABC,EC=$\sqrt{3}$,AB=2.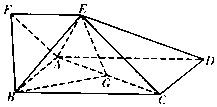 如图,四边形ABCD为矩形,四边形ADEF为梯形,AD∥FE,∠AFE=60°,∠AED=90°,且平面ABCD⊥平面ADEF,AF=FE=AB=$\frac{1}{2}$AD=2,点G为AC的中点.
如图,四边形ABCD为矩形,四边形ADEF为梯形,AD∥FE,∠AFE=60°,∠AED=90°,且平面ABCD⊥平面ADEF,AF=FE=AB=$\frac{1}{2}$AD=2,点G为AC的中点.