题目内容

2．已知集合A={x|x2-2x＜0}，B={y|y=|x|+1，x∈R}，则A∩∁RB=（　　）
A．（0，2）B．[1，2）C．（0，1]D．（0，1）

分析 求解不等式可得集合A，求B的值域可得集合B，根据集合的基本运算即可求A∩∁RB．

解答 解：由不等式x2-2x＜0
解得：0＜x＜2
∴集合A={x|0＜x＜2}，
由函数y=|x|+1，x∈R，可得值域为[1+∞），
∴集合B=[1+∞），
∴∁RB=（-∞，1）．
那么：A∩∁RB=（0，1）
故选D

点评 本题考查了不等式的计算，值域的问题和集合的基本运算，比较基础．

练习册系列答案
相关题目
12．已知函数f（x）=$\left\{\begin{array}{l}{sin\frac{πx}{6}，0≤x≤2}\\{2f（x-2），x＞2}\end{array}\right.$，则f（2017）等于（　　）
A．0B．$\frac{1}{2}$C．21007D．21008
13．已知平面向量$\overrightarrow a，\overrightarrow b$的夹角为 120°，且$|{\overrightarrow a}|=1，|{\overrightarrow b}|=2$．若平面向量 $\overrightarrow m$满足$\overrightarrow m•\overrightarrow a=\overrightarrow m•\overrightarrow b=1$，则$|{\overrightarrow m}|$=$\frac{\sqrt{21}}{3}$．
10．已知$P：{x^2}-2x＜0，Q：\frac{x+3}{x-1}≤0$，若P真Q假，则x的取值范围是（　　）
A．[1，2）B．（1，2）C．（-∞，-3）D．（-∞，-3]
17．设函数f（x）=ln（x+1）-$\frac{kx}{x+1}$+1（x＞-1）
（1）讨论f（x）的单调性；
（2）k＞0，若f（x）的最小值为g（k），当0＜k1＜k2且k1+k2=2，比较g（k1）与g（k2）的大小．
7．已知函数$f（x）=\left\{\begin{array}{l}{log_5}（{1-x}）（{x＜1}）\\-{（{x-2}）^2}+2（{x≥1}）\end{array}\right.$，则关于x的方程$f（{x+\frac{1}{x}-2}）=a$，当1＜a＜2时实根个数为（　　）
A．5个B．6个C．7个D．8个
14．数列{an}满足a1=1，且an+1=a1+an+n（n∈N*），则$\frac{1}{a_1}+\frac{1}{a_2}+$…$+\frac{1}{{{a_{2016}}}}$等于（　　）
A．$\frac{4032}{2017}$B．$\frac{4028}{2015}$C．$\frac{2015}{2016}$D．$\frac{2014}{2015}$
11．设集合A={x|（x-1）（x-3）＜0}，B={y|y=2x，x∈[1，2]}，则A∩B=（　　）
A．∅B．（1，3）C．[2，3）D．（1，4]
12．一个几何体的三视图如图所示，则该几何体的体积为（　　）
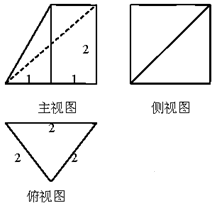
A．2$\sqrt{3}$B．$\sqrt{3}$C．$\frac{{4\sqrt{3}}}{3}$D．$\frac{{2\sqrt{3}}}{3}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网