题目内容
函数f（x）=2xlog2e-2lnx-ax+3的一个极值点在区间（1，2）内，则实数a的取值范围是（ ）
| A、（1，3） |
| B、（1，2） |
| C、（0，3） |
| D、（0，2） |
考点：利用导数研究函数的极值
专题：计算题,导数的综合应用
分析：求导f′（x）=2x-2
-a，注意到其在（1，2）上是增函数，故可得f′（1）f′（2）＜0，从而解得．
| 1 |
| x |
解答：
解：∵f′（x）=2x-2
-a在（1，2）上是增函数，
∴若使函数f（x）=2xlog2e-2lnx-ax+3的一个极值点在区间（1，2）内，
则f′（1）f′（2）＜0，
即（-a）（3-a）＜0，
解得，0＜a＜3，
故选C．
| 1 |
| x |
∴若使函数f（x）=2xlog2e-2lnx-ax+3的一个极值点在区间（1，2）内，
则f′（1）f′（2）＜0，
即（-a）（3-a）＜0，
解得，0＜a＜3，
故选C．
点评：本题考查了导数的综合应用，同时考查了极值的定义，属于中档题．
练习册系列答案
相关题目
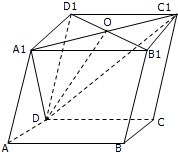如图所示，在平行六面体ABCD-A1B1C1D1中，O是B1D1的中点，求证：
某几何体的三视图如图所示，其中正视图和左视图的上半部分均为边长为2的等边三角形，则该几何体的体积为