题目内容
6.已知正方体ABCD-A1B1C1D1,平面α过直线BD,α⊥平面AB1C,α∩平面AB1C=m,平面β过直线A1C1,β∥平面AB1C,β∩平面ADD1A1=n,则m,n所成角的余弦值为( )| A. | 0 | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
分析 如图所示,BD1⊥平面AB1C,平面α过直线BD,α⊥平面AB1C,可得平面α即为平面DBB1D1.设AC∩BD=O.可得α∩平面AB1C=m为OB1.同理可得:平面A1C1D即为平面β.又A1D∥B1C,可得m,n所成角为∠OB1C,根据△AB1C为正三角形,即可得出.
解答 解:如图所示,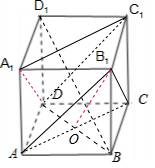
∵BD1⊥平面AB1C,平面α过直线BD,α⊥平面AB1C,
∴平面α即为平面DBB1D1.设AC∩BD=O.
∴α∩平面AB1C=m为OB1.
∵平面A1C1D过直线A1C1,与平面AB1C平行,
而平面β过直线A1C1,β∥平面AB1C,
∴平面A1C1D即为平面β.
β∩平面ADD1A1=A1D=n,
又A1D∥B1C,
∴m,n所成角为∠OB1C,
由△AB1C为正三角形,则cos∠OB1C=cos$\frac{π}{6}$=$\frac{\sqrt{3}}{2}$.
故选:D.
点评 本题考查了正方体的性质、空间位置关系、等边三角形的性质、空间角,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
16.已知椭圆E的左、右焦点分别为F1,F2,过F1且斜率为2的直线交椭圆E于P,Q两点,若$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}=0$,则椭圆E的离心率为( )
| A. | $\frac{{\sqrt{5}}}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{{\sqrt{2}}}{3}$ | D. | $\frac{1}{3}$ |
17.下列函数中,图象的一部分如右图所示的是( )
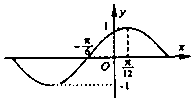

| A. | $y=sin({x+\frac{π}{6}})$ | B. | $y=cos({2x-\frac{π}{6}})$ | C. | $y=sin({2x-\frac{π}{6}})$ | D. | $y=cos({4x-\frac{π}{3}})$ |
1.某几何体的三视图如图所示,则该几何体的体积是( )
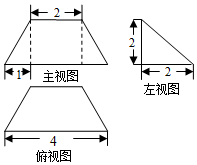

| A. | 4 | B. | $\frac{16}{3}$ | C. | $\frac{20}{3}$ | D. | 12 |
16.执行如图所示的程序框图,当a=2,b=3时,输出s值为( )


| A. | 6 | B. | 8 | C. | 24 | D. | 36 |
 如图,已知斜三棱柱ABC-A1B1C1的所有棱长均为2,∠B1BA=$\frac{π}{3}$,M,N分别为A1C1与B1C的中点,且侧面ABB1A1⊥底面ABC.
如图,已知斜三棱柱ABC-A1B1C1的所有棱长均为2,∠B1BA=$\frac{π}{3}$,M,N分别为A1C1与B1C的中点,且侧面ABB1A1⊥底面ABC.