题目内容
16. 如图,三棱柱ABC-DEF中,侧面ABED是边长为2的菱形,且∠ABE=$\frac{π}{3}$,BC=$\frac{\sqrt{21}}{2}$,点F在平面ABED内的正投影为G,且G在AE上,FG=$\sqrt{3}$,点M在线段CF上,且CM=$\frac{1}{4}$CF.
如图,三棱柱ABC-DEF中,侧面ABED是边长为2的菱形,且∠ABE=$\frac{π}{3}$,BC=$\frac{\sqrt{21}}{2}$,点F在平面ABED内的正投影为G,且G在AE上,FG=$\sqrt{3}$,点M在线段CF上,且CM=$\frac{1}{4}$CF.(1)证明:直线GM∥平面DEF;
(2)求三棱锥M-DEF的体积.
分析 (1)由已知可得AE=2,求解直角三角形可得EG=$\frac{3}{2}$,则AG:HG=1:3,过G作SH∥AD,交AB于S,交DE于H,则SG:GH=1:3,再由已知可得CM:MF=1:3,得到MG∥FH,由线面平行的判定可得直线GM∥平面DEF;
(2)设过MG且平行于平面DEF的平面交三棱柱于MNK,得三棱柱DEF-MNK,可得${V}_{M-DEF}=\frac{1}{3}{V}_{DEF-KMN}$=VM-NEK,由等积法求得三棱锥M-DEF的体积.
解答 (1)证明:如图,∵面ABED是边长为2的菱形,且∠ABE=$\frac{π}{3}$,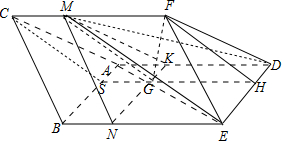
∴△ABE为正三角形,且AE=2,
∵FG⊥GE,FG=$\sqrt{3}$,EF=BC=$\frac{\sqrt{21}}{2}$,
∴EG=$\frac{3}{2}$,则AG:HG=1:3,过G作SH∥AD,
交AB于S,交DE于H,
则SG:GH=1:3,
连接CS、FH,∵CM=$\frac{1}{4}$CF,∴CM:MF=1:3,
∴MG∥FH,又FH?平面DEF,MG?平面DEF,
∴直线GM∥平面DEF;
(2)解:设过MG且平行于平面DEF的平面交三棱柱于MNK,
得三棱柱DEF-MNK,可得${V}_{M-DEF}=\frac{1}{3}{V}_{DEF-KMN}$=VM-NEK,
∵NK=2,NE=$\frac{3}{4}BE=\frac{3}{2}$,∴${S}_{△NEK}=\frac{1}{2}×2×\frac{3}{2}×sin\frac{π}{3}=\frac{3\sqrt{3}}{4}$.
则${V}_{M-NEK}=\frac{1}{3}×\frac{3\sqrt{3}}{4}×\sqrt{3}=\frac{3}{4}$.
点评 本题考查线面平行的判定,考查了空间想象能力和思维能力,训练了利用等积法求多面体的体积,是中档题.

| A. | 平面DD1C1C | B. | 平面A1DB | C. | 平面A1B1C1D1 | D. | 平面A1DB1 |
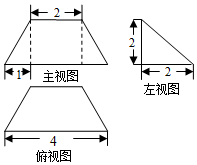
| A. | 4 | B. | $\frac{16}{3}$ | C. | $\frac{20}{3}$ | D. | 12 |
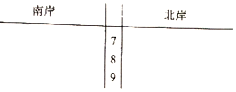 为了响应我市“创建宜居港城,建设美丽莆田”,某环保部门开展以“关爱木兰溪,保护母亲河”为主题的环保宣传活动,经木兰溪流经河段分成10段,并组织青年干部职工对每一段的南、北两岸进行环保综合测评,得到分值数据如表:
为了响应我市“创建宜居港城,建设美丽莆田”,某环保部门开展以“关爱木兰溪,保护母亲河”为主题的环保宣传活动,经木兰溪流经河段分成10段,并组织青年干部职工对每一段的南、北两岸进行环保综合测评,得到分值数据如表:| 南岸 | 77 | 92 | 84 | 86 | 74 | 76 | 81 | 71 | 85 | 87 |
| 北岸 | 72 | 87 | 78 | 83 | 83 | 85 | 75 | 89 | 90 | 95 |
(2)根据表中的数据完成茎叶图:
(3)分别估计两岸分值的中位数,并计算它们的平均数,试从计算结果分析两岸环保情况,哪边保护更好?
| A. | [ln2,ln$\frac{3}{2}$+$\frac{1}{3}$] | B. | (ln2,ln$\frac{3}{2}$+$\frac{1}{3}$) | C. | ($\frac{2}{3}$,ln2] | D. | ($\frac{2}{3}$,ln$\frac{3}{2}$+$\frac{1}{3}$] |
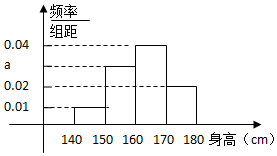 某中学对高三年级进行身高统计,测量随机抽取的20名学生的身高,其频率分布直方图如图(单位:cm)
某中学对高三年级进行身高统计,测量随机抽取的20名学生的身高,其频率分布直方图如图(单位:cm)