题目内容
12.化为推出一款6寸大屏手机,现对500名该手机使用者(200名女性,300名男性)进行调查,对手机进行打分,打分的频数分布表如下:女性用户:
| 分值区间 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100) |
| 频数 | 20 | 40 | 80 | 50 | 10 |
| 分值区间 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100) |
| 频数 | 45 | 75 | 90 | 60 | 30 |
| 女性用户 | 男性用户 | 合计 | |
| “认可”手机 | 140 | 180 | 320 |
| “不认可”手机 | 60 | 120 | 180 |
| 合计 | 200 | 300 | 500 |
| P(K2≥k) | 0.05 | 0.01 |
| k | 3.841 | 6.635 |
(2)根据评分的不同,运用分层抽样从男性用户中抽取20名用户,在这20名用户中,从评分不低于80分的用户中任意抽取2名用户,求2名用户中评分小于90分的概率.
分析 (1)从频数分布表算出女性用户中“认可”手机人数与“不认可”手机人数,填入表格即可;
同理算出男性用户中“认可”手机人数与“不认可”手机人数,填入表格,可得2×2列联表,
由公式计算出K2的值与临界值中数据比较即可;
(2)评分不低于80分有6人,其中评分小于90分的人数为4,记为A、B、C、D,
评分不小于90分的人数为2,记为a、b,
写出从6人中任取2人的所有基本事件,从中找出两名用户评分都小于90分的基本事件,即可求其概率.
解答 解:(1)由频数分布表可得2×2列联表如下图:
| 女性用户 | 男性用户 | 合计 | |
| “认可”手机 | 140 | 180 | 320 |
| “不认可”手机 | 60 | 120 | 180 |
| 合计 | 200 | 300 | 500 |
(2)运用分层抽样从男性用户中抽取20名用户,评分不低于80分有6人,其中评分小于90分的人数为4,
记为A、B、C、D,评分不小于90分的人数为2,记为a、b,从6人中任取2人,
基本事件空间为Ω={AB,AC,AD,Aa,Ab,BC,BD,Ba,Bb,CD,Ca,Cb,Da,Db,ab},
符合条件的共有15个元素,其中把“两名用户评分都小于90分”记作M,
则M={AB,AC,AD,BC,BD,CD}共有6个元素;
所有两名用户评分都小于90分的概率为P=$\frac{6}{15}$=$\frac{2}{5}$.
点评 本题考查了对立性检验和古典概型的概率计算问题,是基础题目.

练习册系列答案
相关题目
3.运行图中的程序框图,若输出的结果为57,则判断框内的条件应为( )


| A. | k>4? | B. | k≤5? | C. | k>3? | D. | k≤4? |
17.下列函数中,图象的一部分如右图所示的是( )
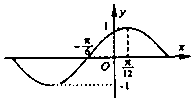

| A. | $y=sin({x+\frac{π}{6}})$ | B. | $y=cos({2x-\frac{π}{6}})$ | C. | $y=sin({2x-\frac{π}{6}})$ | D. | $y=cos({4x-\frac{π}{3}})$ |
1.某几何体的三视图如图所示,则该几何体的体积是( )
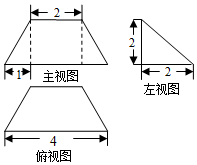

| A. | 4 | B. | $\frac{16}{3}$ | C. | $\frac{20}{3}$ | D. | 12 |
2.圆柱的轴截面是正方形,且轴截面面积是5,则它的侧面积是( )
| A. | π | B. | 5π | C. | 10π | D. | 20π |
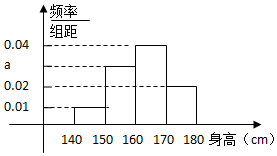 某中学对高三年级进行身高统计,测量随机抽取的20名学生的身高,其频率分布直方图如图(单位:cm)
某中学对高三年级进行身高统计,测量随机抽取的20名学生的身高,其频率分布直方图如图(单位:cm)