题目内容
9.若$f(x)=\left\{\begin{array}{l}f(x-4),x>0\\{2^x}+\int_{\;0}^{\;\frac{π}{6}}{cos3xdx,x≤0}\end{array}\right.$,则f(2016)=$\frac{4}{3}$.分析 由已知得f(2016)=f(0)=${2}^{0}+{∫}_{0}^{\frac{π}{6}}cos3xdx$=1+$\frac{1}{3}$${∫}_{0}^{\frac{π}{6}}cos3xd(3x)$,由此能求出结果.
解答 解:∵$f(x)=\left\{\begin{array}{l}f(x-4),x>0\\{2^x}+\int_{\;0}^{\;\frac{π}{6}}{cos3xdx,x≤0}\end{array}\right.$,
∴f(2016)=f(0)=${2}^{0}+{∫}_{0}^{\frac{π}{6}}cos3xdx$
=1+$\frac{1}{3}$${∫}_{0}^{\frac{π}{6}}cos3xd(3x)$=1+$\frac{1}{3}$×$sin3{x|}_{0}^{\frac{π}{6}}$=1+$\frac{1}{3}=\frac{4}{3}$.
故答案为:$\frac{4}{3}$.
点评 本题考是函数值的求法,是基础题,解题时要认真审题,注意函数性质、定积分知识的合理运用.

练习册系列答案
 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
20.在△ABC中,角A,B,C的对边分别是a,b,c,已知$b=2,c=2\sqrt{2}$,且$C=\frac{π}{4}$,则△ABC的面积为( )
| A. | $\sqrt{3}+1$ | B. | $\sqrt{3}-1$ | C. | 4 | D. | 2 |
17.在△ABC中,$∠A=\frac{π}{3},BC=4\sqrt{3}$,则△ABC的周长为( )
| A. | $4\sqrt{3}+8\sqrt{3}sin(B+\frac{π}{6})$ | B. | $4\sqrt{3}+8sin(B+\frac{π}{3})$ | C. | $4\sqrt{3}+8\sqrt{3}cos(B+\frac{π}{6})$ | D. | $4\sqrt{3}+8cos(B+\frac{π}{3})$ |
18.已知等差数列{an}的前n项和为Sn,且2S3-3S2=15,则数列{an}的公差为( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
19.圆${C_1}:{x^2}+{y^2}+2x+2y-2=0$与圆${C_2}:{x^2}+{y^2}-4x-2y+4=0$的公切线有( )
| A. | .1条 | B. | .2条 | C. | .3条 | D. | .4条 |
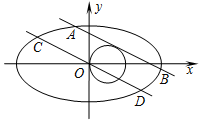 已知椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{{\sqrt{3}}}{2}$,且过点$({2,\sqrt{3}}))$,直线l1:y=kx+m(m>0)与圆C2:(x-1)2+y2=1相切且与椭圆C1交于A,B两点.
已知椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{{\sqrt{3}}}{2}$,且过点$({2,\sqrt{3}}))$,直线l1:y=kx+m(m>0)与圆C2:(x-1)2+y2=1相切且与椭圆C1交于A,B两点.