题目内容
已知函数f（x）是定义在[-4，0）∪（0，4]上的奇函数，当时，f（x）的图象如图所示，那么f（x）的值域是（ ）| A、（-4，4） |
| B、[-6，6] |
| C、（-4，4）∪（4，6] |
| D、[-6，-4）∪（4，6] |
考点：函数奇偶性的性质
专题：函数的性质及应用
分析：根据函数奇偶性的性质，确定函数的值域即可．
解答：
解：∵当0＜x≤4时，函数单调递增，由图象知4＜f（x）≤6，
当-4≤x＜0时，在0＜-x≤4，即此时函数也单调递增，
且4＜f（-x）≤6，
∵函数是奇函数，
∴f（-x）=-f（x），
∴4＜-f（x）≤6，
即-6≤f（x）＜-4，
∴f（x）的值域是[-6，-4）∪（4，6]，
故选：D
当-4≤x＜0时，在0＜-x≤4，即此时函数也单调递增，
且4＜f（-x）≤6，
∵函数是奇函数，
∴f（-x）=-f（x），
∴4＜-f（x）≤6，
即-6≤f（x）＜-4，
∴f（x）的值域是[-6，-4）∪（4，6]，
故选：D
点评：本题主要考查函数值域的求法，利用函数奇偶性的性质进行转化是解决本题的关键．
练习册系列答案
相关题目
某几何体的三视图如图所示，则该几何体的表面积（ ）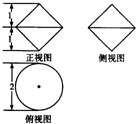
A、
| ||
B、2
| ||
C、（2
| ||
D、（2
|
若等比数列{an}的前3项的和S3=14，且a2=4，公比大于1，则a7=（ ）
| A、182 | B、46 |
| C、64 | D、128 |