题目内容
函数y=2x+1(x<0)的反函数是 .
考点:反函数
专题:函数的性质及应用
分析:由已知得到2x=y-1,化指数式为对数式后把x,y互换求得原函数的反函数.
解答:
解:由y=2x+1(x<0),得2x=y-1,
则x=log2(y-1)(1<y<2),
把x,y互换得y=log2(x-1)(1<x<2).
∴函数y=2x+1(x<0)的反函数是y=log2(x-1)(1<x<2).
故答案为:y=log2(x-1)(1<x<2).
则x=log2(y-1)(1<y<2),
把x,y互换得y=log2(x-1)(1<x<2).
∴函数y=2x+1(x<0)的反函数是y=log2(x-1)(1<x<2).
故答案为:y=log2(x-1)(1<x<2).
点评:求反函数,一般应分以下步骤:(1)由已知解析式y=f(x)反求出x=Ф(y);(2)交换x=Ф(y)中x、y的位置;(3)求出反函数的定义域(一般可通过求原函数的值域的方法求反函数的定义域)是基础题.

练习册系列答案
相关题目
某几何体的三视图如图所示,则该几何体的体积为( )


| A、16+8π |
| B、8+8π |
| C、16+16π |
| D、8+16π |
如程序框图运行结果是( )


| A、11 | B、8 | C、5 | D、13 |
执行如图程序框图,那么输出S的值为( )


A、
| ||
B、
| ||
C、
| ||
D、
|
 已知函数f(x)是定义在[-4,0)∪(0,4]上的奇函数,当时,f(x)的图象如图所示,那么f(x)的值域是( )
已知函数f(x)是定义在[-4,0)∪(0,4]上的奇函数,当时,f(x)的图象如图所示,那么f(x)的值域是( )| A、(-4,4) |
| B、[-6,6] |
| C、(-4,4)∪(4,6] |
| D、[-6,-4)∪(4,6] |
如果函数y=cos(x+φ)的一个零点是
,那么φ可以是( )
| π |
| 3 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
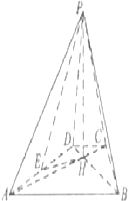 如图,已知四棱锥P-ABCD的底面为等腰梯形,AB∥CD,AC⊥BD垂足为H,PH是四棱锥的高,E为AD的中点.
如图,已知四棱锥P-ABCD的底面为等腰梯形,AB∥CD,AC⊥BD垂足为H,PH是四棱锥的高,E为AD的中点.