题目内容
某几何体的三视图如图所示，则该几何体的表面积（ ）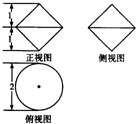
A、
| ||
B、2
| ||
C、（2
| ||
D、（2
|
考点：由三视图求面积、体积
专题：空间位置关系与距离
分析：根据几何体的三视图，得出该几何体是上、下部为共底面的圆锥体的组合体，从而求出它的表面积．
解答：
解：根据几何体的三视图，得；
该几何体是上、下部为共底面的圆锥体的组合体；
该圆锥的底面半径为1，高为1；
∴该几何体的表面积为
S=2×π•1•
=2
π．
故选：B．
该几何体是上、下部为共底面的圆锥体的组合体；
该圆锥的底面半径为1，高为1；
∴该几何体的表面积为
S=2×π•1•
| 12+12 |
| 2 |
故选：B．
点评：本题考查了空间几何体的三视图的应用问题，是基础题目．
练习册系列答案
相关题目
双曲线y2-3x2=9的渐近线方程为（ ）
A、x±
| ||
| B、x±3y=0 | ||
C、
| ||
| D、3x±y=0 |
已知平面a⊥平面β，a∩β=l，点A∈a，A∉l，直线AB∥β，直线AC⊥l，直线AD⊥β，则下列四种位置关系中，不一定成立的是（ ）
| A、AB∥l | B、AC⊥AB |
| C、AD与l相交 | D、AC⊥β |
某几何体的三视图如图所示，则该几何体的体积为（ ）
| A、16+8π |
| B、8+8π |
| C、16+16π |
| D、8+16π |
如程序框图运行结果是（ ）
| A、11 | B、8 | C、5 | D、13 |
已知函数f（x）是定义在[-4，0）∪（0，4]上的奇函数，当时，f（x）的图象如图所示，那么f（x）的值域是（ ）| A、（-4，4） |
| B、[-6，6] |
| C、（-4，4）∪（4，6] |
| D、[-6，-4）∪（4，6] |