题目内容
 如图所示,直棱柱ABCD-A1B1C1D1中,底面ABCD是直角梯形,∠BAD=∠ADC=90°,AB=2AD=2CD=2.
如图所示,直棱柱ABCD-A1B1C1D1中,底面ABCD是直角梯形,∠BAD=∠ADC=90°,AB=2AD=2CD=2.(Ⅰ)若P是A1B1的中点,求证:DP∥平面ACB1平行;
(Ⅱ)求证:平面ACC1A1⊥平面BB1C1C.
考点:平面与平面垂直的判定
专题:综合题,空间位置关系与距离
分析:(Ⅰ)由P为A1B1的中点,知PB1∥AB,且PB1=
AB,证明DCB1P为平行四边形,从而CB1∥DP,即可证明DP∥平面ACB1平行;
(Ⅱ)直棱柱ABCD-A1B1C1D1中,由BB1⊥平面ABCD,知BB1⊥AC,有∠BAD=∠ADC=90°,知AB=2AD=2CD=2,由此能够证明AC⊥平面BB1C1C,即可证明平面ACC1A1⊥平面BB1C1C.
| 1 |
| 2 |
(Ⅱ)直棱柱ABCD-A1B1C1D1中,由BB1⊥平面ABCD,知BB1⊥AC,有∠BAD=∠ADC=90°,知AB=2AD=2CD=2,由此能够证明AC⊥平面BB1C1C,即可证明平面ACC1A1⊥平面BB1C1C.
解答:
证明:(Ⅰ)由P为A1B1的中点,知PB1∥AB,且PB1=
AB,
∵DC∥AB,DC=
AB,
∴DC∥PB1,且DC=PB1,
∴DCB1P为平行四边形,从而CB1∥DP,
∵CB1?面ACB1,DP?面ACB1,
∴DP∥面ACB1.
(Ⅱ)直棱柱ABCD-A1B1C1D1中,BB1⊥平面ABCD,
∴BB1⊥AC,
∵∠BAD=∠ADC=90°,AB=2AD=2CD=2,
∴AC=
,∴BC=
,∴BC⊥AC,
∴AC⊥平面BB1C1C,
又AC?平面ACC1A1,
∴平面ACC1A1⊥平面BB1C1C. …(13分)
| 1 |
| 2 |
∵DC∥AB,DC=
| 1 |
| 2 |
∴DC∥PB1,且DC=PB1,
∴DCB1P为平行四边形,从而CB1∥DP,
∵CB1?面ACB1,DP?面ACB1,
∴DP∥面ACB1.
(Ⅱ)直棱柱ABCD-A1B1C1D1中,BB1⊥平面ABCD,
∴BB1⊥AC,
∵∠BAD=∠ADC=90°,AB=2AD=2CD=2,
∴AC=
| 2 |
| 2 |
∴AC⊥平面BB1C1C,
又AC?平面ACC1A1,
∴平面ACC1A1⊥平面BB1C1C. …(13分)
点评:本题考查直线与平面垂直的证明和直线与平面平行的证明,解题时要认真审题,仔细解答,注意合理地化空间问题为平面问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
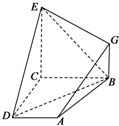 如图,已知四边形ABCD和BCEG均为直角梯形,AD∥BC,CE∥BG,且∠BCD=∠BCE=
如图,已知四边形ABCD和BCEG均为直角梯形,AD∥BC,CE∥BG,且∠BCD=∠BCE= 如图,已知四棱锥P-ABCD的底面是矩形,侧面PAB是正三角形,且平面PAB⊥平面ABCD,E是PA的中点,AC与BD的交点为M.
如图,已知四棱锥P-ABCD的底面是矩形,侧面PAB是正三角形,且平面PAB⊥平面ABCD,E是PA的中点,AC与BD的交点为M.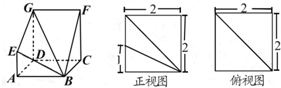 如图,多面体ABCD-EFG中,底面ABCD为正方形,GD∥FC∥AE,AE⊥平面ABCD,其正视图、俯视图及相关数据如图:
如图,多面体ABCD-EFG中,底面ABCD为正方形,GD∥FC∥AE,AE⊥平面ABCD,其正视图、俯视图及相关数据如图: