题目内容
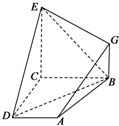 如图,已知四边形ABCD和BCEG均为直角梯形,AD∥BC,CE∥BG,且∠BCD=∠BCE=
如图,已知四边形ABCD和BCEG均为直角梯形,AD∥BC,CE∥BG,且∠BCD=∠BCE=| π |
| 2 |
(Ⅰ)EC⊥CD;
(Ⅱ)求证:AG∥平面BDE;
(Ⅲ)求:几何体EG-ABCD的体积.
考点:棱柱、棱锥、棱台的体积,直线与平面平行的判定
专题:综合题,空间位置关系与距离
分析:(Ⅰ)利用面面垂直的性质,证明EC⊥平面ABCD,利用线面垂直的性质证明EC⊥CD;
(Ⅱ)在平面BCEG中,过G作GN⊥CE交BE于M,连DM,证明四边形ADMG为平行四边形,可得AG∥DM,即可证明AG∥平面BDE;
(Ⅲ)利用分割法即可求出几何体EG-ABCD的体积.
(Ⅱ)在平面BCEG中,过G作GN⊥CE交BE于M,连DM,证明四边形ADMG为平行四边形,可得AG∥DM,即可证明AG∥平面BDE;
(Ⅲ)利用分割法即可求出几何体EG-ABCD的体积.
解答:
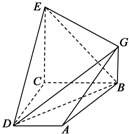 (Ⅰ)证明:由平面ABCD⊥平面BCEG,
(Ⅰ)证明:由平面ABCD⊥平面BCEG,
平面ABCD∩平面BCEG=BC,CE⊥BC,CE?平面BCEG,
∴EC⊥平面ABCD,…(3分)
又CD?平面BCDA,故EC⊥CD…(4分)
(Ⅱ)证明:在平面BCEG中,过G作GN⊥CE交BE于M,连DM,
则由已知知;MG=MN,MN∥BC∥DA,且MN=AD=
BC,
∴MG∥AD,MG=AD,故四边形ADMG为平行四边形,∴AG∥DM…(6分)
∵DM?平面BDE,AG?平面BDE,∴AG∥平面BDE…(8分)
(Ⅲ)解:VEG-ABCD=VD-BCEG+VG-ABD=
SBCEG•DC+
S△ABD•BG…(10分)
=
×
×2×2+
×
×1×2×1=
…(12分)
 (Ⅰ)证明:由平面ABCD⊥平面BCEG,
(Ⅰ)证明:由平面ABCD⊥平面BCEG,平面ABCD∩平面BCEG=BC,CE⊥BC,CE?平面BCEG,
∴EC⊥平面ABCD,…(3分)
又CD?平面BCDA,故EC⊥CD…(4分)
(Ⅱ)证明:在平面BCEG中,过G作GN⊥CE交BE于M,连DM,
则由已知知;MG=MN,MN∥BC∥DA,且MN=AD=
| 1 |
| 2 |
∴MG∥AD,MG=AD,故四边形ADMG为平行四边形,∴AG∥DM…(6分)
∵DM?平面BDE,AG?平面BDE,∴AG∥平面BDE…(8分)
(Ⅲ)解:VEG-ABCD=VD-BCEG+VG-ABD=
| 1 |
| 3 |
| 1 |
| 3 |
=
| 1 |
| 3 |
| 2+1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 7 |
| 3 |
点评:本题考查面面垂直、线面平行,考查几何体体积的计算,考查学生分析解决问题的能力,正确运用面面垂直、线面平行的判定定理是关键.

练习册系列答案
相关题目
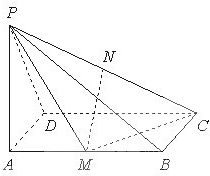 如图,已知PA⊥矩形ABCD所在的平面,M、N分别为AB、PC的中点,∠PDA=45°,AB=2,AD=1.
如图,已知PA⊥矩形ABCD所在的平面,M、N分别为AB、PC的中点,∠PDA=45°,AB=2,AD=1. 如图所示,直棱柱ABCD-A1B1C1D1中,底面ABCD是直角梯形,∠BAD=∠ADC=90°,AB=2AD=2CD=2.
如图所示,直棱柱ABCD-A1B1C1D1中,底面ABCD是直角梯形,∠BAD=∠ADC=90°,AB=2AD=2CD=2.