题目内容
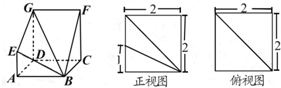 如图,多面体ABCD-EFG中,底面ABCD为正方形,GD∥FC∥AE,AE⊥平面ABCD,其正视图、俯视图及相关数据如图:
如图,多面体ABCD-EFG中,底面ABCD为正方形,GD∥FC∥AE,AE⊥平面ABCD,其正视图、俯视图及相关数据如图:(1)求证:平面AEFC⊥平面BDG;
(2)求该几何体的体积;
(3)求点C到平面BDG的距离.
考点:平面与平面垂直的判定,棱柱、棱锥、棱台的体积,点、线、面间的距离计算
专题:空间位置关系与距离
分析:(1)由面面垂直的判定定理,先证线面垂直,再证面面垂直,即证明AC⊥面BDG;
(2)原几何体可以划分为两个四棱锥:B-CFGD和B-AEGD;
(3)过C作CH⊥BD于H,则CH⊥平面BDG,故CH的长即为点C到平面BDG的距离,利用等面积,即可求得结论.
(2)原几何体可以划分为两个四棱锥:B-CFGD和B-AEGD;
(3)过C作CH⊥BD于H,则CH⊥平面BDG,故CH的长即为点C到平面BDG的距离,利用等面积,即可求得结论.
解答:
(1)证明:连接AC,BD,
正方形ABCD中,AC⊥BD,又AE∥GD∥FC,AE⊥平面ABCD,
∴GD⊥平面ABCD,
又AC?平面ABCD,则AC⊥GD,
又AC⊥BD,GD∩BD=D,
∴AC⊥平面BDG,
又AC?平面AEFC,∴平面AEFC⊥平面BDG;
(2)解:原几何体可以划分为两个四棱锥:B-CFGD和B-AEGD,而
VB-CFGD=
•22•2=
,VB-AEGD=
•
(1+2)•2•2=2,
∴所给几何体的体积为:V=
+2=
;
(3)解:由条件可知GD⊥平面ABCD,故平面BDG⊥平面ABCD.
过C作CH⊥BD于H,则CH⊥平面BDG,故CH的长即为点C到平面BDG的距离.
在Rt△BCD中,由面积公式可得BD•CH=BC•CD,则CH=
,
即点C到平面BDG的距离为
.
正方形ABCD中,AC⊥BD,又AE∥GD∥FC,AE⊥平面ABCD,
∴GD⊥平面ABCD,
又AC?平面ABCD,则AC⊥GD,
又AC⊥BD,GD∩BD=D,
∴AC⊥平面BDG,
又AC?平面AEFC,∴平面AEFC⊥平面BDG;
(2)解:原几何体可以划分为两个四棱锥:B-CFGD和B-AEGD,而
VB-CFGD=
| 1 |
| 3 |
| 8 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
∴所给几何体的体积为:V=
| 8 |
| 3 |
| 14 |
| 3 |
(3)解:由条件可知GD⊥平面ABCD,故平面BDG⊥平面ABCD.
过C作CH⊥BD于H,则CH⊥平面BDG,故CH的长即为点C到平面BDG的距离.
在Rt△BCD中,由面积公式可得BD•CH=BC•CD,则CH=
| 2 |
即点C到平面BDG的距离为
| 2 |
点评:本题考查了立体几何中面面垂直的判定定理,考查体积的计算,考查点C到平面BDG的距离,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图所示,直棱柱ABCD-A1B1C1D1中,底面ABCD是直角梯形,∠BAD=∠ADC=90°,AB=2AD=2CD=2.
如图所示,直棱柱ABCD-A1B1C1D1中,底面ABCD是直角梯形,∠BAD=∠ADC=90°,AB=2AD=2CD=2.