题目内容
如图，已知四棱锥P-ABCD的底面是矩形，侧面PAB是正三角形，且平面PAB⊥平面ABCD，E是PA的中点，AC与BD的交点为M．（1）求证：PC∥平面EBD；
（2）求证：BE⊥平面AED．
考点：直线与平面平行的判定,直线与平面垂直的判定
专题：空间位置关系与距离
分析：（1）连结EM，由三角形中位线定理能证明PC∥平面EBD．
（2）由已知条件得AD⊥平面PAB，从而得到AD⊥BE，由等边三角形性质得BE⊥AE，由此能证明BE⊥平面AED．
（2）由已知条件得AD⊥平面PAB，从而得到AD⊥BE，由等边三角形性质得BE⊥AE，由此能证明BE⊥平面AED．
解答：
（1）证明：连结EM，∵四边形ABCD是矩形，∴M为AC的中点，
∵E是PA的中点，∴EM是△PAC的中位线，
∴EM∥PC，
∵EM?平面EBD，PC不包含于平面EBD，
∴PC∥平面EBD．
（2）∵平面PAB⊥平面ABCD，平面PAB∩平面ABCD=AB，
而AD⊥AB，∴AD⊥平面PAB，
∵BE?平面PAB，∴AD⊥BE，
又∵△PAB是等边三角形，且E是PA的中点，
∴BE⊥AE，
又AE∩AD=A，
∴BE⊥平面AED．
∵E是PA的中点，∴EM是△PAC的中位线，
∴EM∥PC，
∵EM?平面EBD，PC不包含于平面EBD，
∴PC∥平面EBD．
（2）∵平面PAB⊥平面ABCD，平面PAB∩平面ABCD=AB，
而AD⊥AB，∴AD⊥平面PAB，
∵BE?平面PAB，∴AD⊥BE，
又∵△PAB是等边三角形，且E是PA的中点，
∴BE⊥AE，
又AE∩AD=A，
∴BE⊥平面AED．
点评：本题考查直线与平面平行的证明，考查直线与平面垂直的证明，解题时要认真审题，注意空间思维能力的培养．
练习册系列答案
第三学期赢在暑假系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
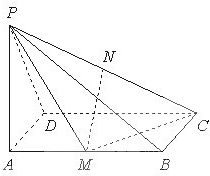如图，已知PA⊥矩形ABCD所在的平面，M、N分别为AB、PC的中点，∠PDA=45°，AB=2，AD=1．
如图所示，直棱柱ABCD-A1B1C1D1中，底面ABCD是直角梯形，∠BAD=∠ADC=90°，AB=2AD=2CD=2．
如图，在直三棱柱ABC-A1B1C1中，AC=BC=BB1=2．AB=2
如图，已知四棱锥P-ABCD，底面ABCD是边长为2的菱形，PA⊥平面ABCD，PA=2，∠ABC=60°，E、F分别为BC、PD的中点．