Question

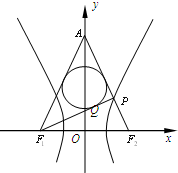如图，已知双曲线

x2

a2

-

y2

b2

=1（a＞0，b＞0）的左、右焦点分别为F₁，F₂，F₁F₂=4，P是双曲线右支上的一点，F₂P与y轴交于点A，△APF₁的内切圆在PF₁上的切点为Q，若PQ=1，则双曲线的离心率是

 

．

Answer 1

考点：双曲线的简单性质

专题：计算题,作图题,圆锥曲线的定义、性质与方程

分析：由圆锥曲线的定义及图中的相等关系推出a，从而求出离心率．

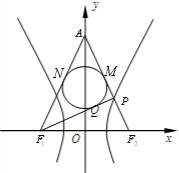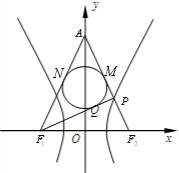解答： 解：如图记AF₁、AF₂与△APF₁的内切圆相切于N、M；
则AN=AM，PM=PQ，NF₁=QF₁，AF₁=AF₂；
则NF₁=AF₁-AN=AF₂-AM=MF₂；
则QF₁=MF₂；
则PF₁-PF₂=（QF₁+PQ）-（MF₂-PM）
=QF₁+PQ-MF₂+PM
=PQ+PM=2PQ=2，
即2a=2，则a=1．
由F₁F₂=4=2c得，c=2；
则e=

c

a

=

2

1

=2．
故答案为：2．

点评：本题考查了学生的作图能力及识图能力，要从图中找到等量关系从而求出a，属于难题．