题目内容
已知△ABC是锐角三角形,且sin(B-
)cos(B-
)=
.
(Ⅰ)求角B的值;
(Ⅱ)求tanAtanC的最小值.
| π |
| 6 |
| π |
| 3 |
| 1 |
| 2 |
(Ⅰ)求角B的值;
(Ⅱ)求tanAtanC的最小值.
考点:三角函数中的恒等变换应用,同角三角函数基本关系的运用,两角和与差的正弦函数
专题:计算题,三角函数的求值
分析:(Ⅰ)利用两角差的正余弦公式展开,结合同角三角函数基本关系式可求出cosB,然后根据△ABC是锐角三角形,求出B;(Ⅱ)根据内角和定理求出A+C,利用两角和的正切公式求tan(A+C),得到关于tanA,tanC和tanAtanC的关系式,然后利用基本不等式求最值.
解答:
解:(Ⅰ)由sin(B-
)cos(B-
)=
,且B为锐角,
变形得:(sinBcos
-cosBsin
)(cosBcos
+sinBsin
)
=(
sinB-
cosB)(
cosB+
sinB)
=
sin2B-
cos2B=
(1-cos2B)-
cos2B
=
-cos2B=
,
整理得:cos2B=
,即cosB=
,
则B=
;
(Ⅱ)∵B=
,∴A+C=
,
又△ABC是锐角三角形,所以tanA>0,tanC>0,
而tan(A+C)=
=-
,
所以
tanAtanC-
=tanA+tanC≥2
,
即
tanAtanC-
≥2
,
得
≥
或
≤-
(舍),
∴tanAtanC≥3,等号仅当tanA=tanC=
,即A=C=
时成立.
∴tanAtanC的最小值为3.
| π |
| 6 |
| π |
| 3 |
| 1 |
| 2 |
变形得:(sinBcos
| π |
| 6 |
| π |
| 6 |
| π |
| 3 |
| π |
| 3 |
=(
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
=
| 3 |
| 4 |
| 1 |
| 4 |
| 3 |
| 4 |
| 1 |
| 4 |
=
| 3 |
| 4 |
| 1 |
| 2 |
整理得:cos2B=
| 1 |
| 4 |
| 1 |
| 2 |
则B=
| π |
| 3 |
(Ⅱ)∵B=
| π |
| 3 |
| 2π |
| 3 |
又△ABC是锐角三角形,所以tanA>0,tanC>0,
而tan(A+C)=
| tanA+tanC |
| 1-tanAtanC |
| 3 |
所以
| 3 |
| 3 |
| tanAtanC |
即
| 3 |
| 3 |
| tanAtanC |
得
| tanAtanC |
| 3 |
| tanAtanC |
| ||
| 3 |
∴tanAtanC≥3,等号仅当tanA=tanC=
| 3 |
| π |
| 3 |
∴tanAtanC的最小值为3.
点评:本题考查了三角恒等变换及求最值问题,综合性较强.解题的关键是明确变形的方向,选择恰当的公式对式子进行适当的变形,在求最值时可以利用基本不等式,注意等号成立的条件.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
某几何体的三视图如图所示,则它的体积是( )


| A、5 | ||
| B、6 | ||
C、
| ||
D、
|
已知复数z满足
=i(i为虚数单位),则z的虚部为( )
| 1+z |
| 1-z |
| A、1 | B、-i | C、i | D、-1 |
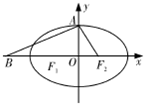 如图,设椭圆C:
如图,设椭圆C: 为增强市民的节能环保意识,某市面向全市征召义务宣传志愿者.从符合条件的500名志愿者中随机抽取100名志愿者,其年龄频率分布直方图如图所示,其中年龄分组区间是:[20,25)[25,30)[30,35)[35,40)[40,45]
为增强市民的节能环保意识,某市面向全市征召义务宣传志愿者.从符合条件的500名志愿者中随机抽取100名志愿者,其年龄频率分布直方图如图所示,其中年龄分组区间是:[20,25)[25,30)[30,35)[35,40)[40,45]