题目内容
15．记函数y=ex在x=n（n=1，2，3，…）处的切线为ln．若切线ln与ln+1的交点坐标为（An，Bn），那么（ ）| A． | 数列{An}是等差数列，数列{Bn}是等比数列 | |
| B． | 数列{An}与{Bn}都是等差数列 | |
| C． | 数列{An}是等比数列，数列{Bn}是等差数列 | |
| D． | 数列{An}与{Bn}都是等比数列 |
分析 求得函数的导数，可得切线的斜率和切点，运用点斜式方程可得切线ln的方程，ln+1的方程，解方程可得An，Bn，再由等差数列和等比数列的通项公式，即可判断．
解答 解：函数y=ex的导数为y′=ex，
可得切线ln的方程为y-en=en（x-n），①
ln+1的方程为y-en+1=en+1（x-n-1），②
由①②解得An=n+$\frac{1}{e-1}$；
Bn=$\frac{{e}^{n+1}}{e-1}$，
即有数列{An}是首项为$\frac{e}{e-1}$，公差为1的等差数列，
数列{Bn}是首项为$\frac{{e}^{2}}{e-1}$，公比为e的等比数列．
故选：A．
点评 本题考查导数的运用：求切线的方程，考查等差数列和等比数列的判断，正确求导和运用点斜式方程是解题的关键，属于中档题．
练习册系列答案
相关题目
7．已知M是圆周上的一个定点，若在圆周上任取一点N，连接MN，则弦MN的长不小于圆半径的概率是（ ）
| A． | $\frac{1}{4}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{2}$ | D． | $\frac{2}{3}$ |
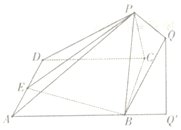已知如图所示的几何体中，四边形ABCD是边长为2的菱形，面PBC⊥面A BCD，点E是AD 的中点，PQ∥面ABCD且点Q在面ABCD上的射影Q′落在AB的延长线上，若PQ=1，PB=$\sqrt{2}$，且（$\overrightarrow{PB}+\overrightarrow{PC}$）•$\overrightarrow{BC}$=0，$\overrightarrow{AB}•\overrightarrow{AD}$=2