题目内容
5.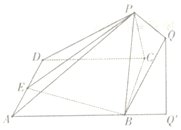 已知如图所示的几何体中,四边形ABCD是边长为2的菱形,面PBC⊥面A BCD,点E是AD 的中点,PQ∥面ABCD且点Q在面ABCD上的射影Q′落在AB的延长线上,若PQ=1,PB=$\sqrt{2}$,且($\overrightarrow{PB}+\overrightarrow{PC}$)•$\overrightarrow{BC}$=0,$\overrightarrow{AB}•\overrightarrow{AD}$=2
已知如图所示的几何体中,四边形ABCD是边长为2的菱形,面PBC⊥面A BCD,点E是AD 的中点,PQ∥面ABCD且点Q在面ABCD上的射影Q′落在AB的延长线上,若PQ=1,PB=$\sqrt{2}$,且($\overrightarrow{PB}+\overrightarrow{PC}$)•$\overrightarrow{BC}$=0,$\overrightarrow{AB}•\overrightarrow{AD}$=2(I )求证面PBC⊥面PBE
(II )求平面PBQ与平面PAD所成钝二面角的正切值.
分析 (I )由已知结合数量积公式可得∠A=60°,再由余弦定理求得BE,可知BE⊥AD,得BE⊥BC,由面面垂直的性质得BE⊥面PBC,再由面面垂直的判定可得面PBC⊥面PBE;
(II )取BC中点O,连接PO、OD,由已知可得PO⊥BC,则PO⊥平面ABCD,有PO⊥OD,再证明OD⊥BC.以O为坐标原点,分别以OC、OD、OP所在直线为x、y、z轴建立空间直角坐标系.结合已知求得B,P,Q,D,A的坐标,进一步求出平面PBQ与平面PAD的一个法向量,由两法向量所成角的余弦值得平面PBQ与平面PAD所成钝二面角的余弦值,进一步求得正切值.
解答 (I )证明:如图,
∵$|\overrightarrow{AB}|=|\overrightarrow{AD}|=2$,$\overrightarrow{AB}•\overrightarrow{AD}$=2,
∴cosA=$\frac{\overrightarrow{AB}•\overrightarrow{AD}}{|\overrightarrow{AB}||\overrightarrow{AD}|}=\frac{2}{2×2}=\frac{1}{2}$,则∠A=60°,
又AE=$\frac{1}{2}AD=1$,则BE2=AB2+AE2-2AB•AE•cos60°=$4+1-2×2×1×\frac{1}{2}=3$.
∴AE2+BE2=AB2,即BE⊥AD,
又AD∥BC,∴BE⊥BC,
∵面PBC⊥面A BCD,且面PBC∩面A BCD=BC,
∴BE⊥面PBC,而BE?面PBE,
∴面PBC⊥面PBE;
(II )解:取BC中点O,连接PO、OD,
∵($\overrightarrow{PB}+\overrightarrow{PC}$)•$\overrightarrow{BC}$=0,∴PO⊥BC,则PO⊥平面ABCD,有PO⊥OD,
∵BE∥OD,BE⊥BC,∴OD⊥BC.
以O为坐标原点,分别以OC、OD、OP所在直线为x、y、z轴建立空间直角坐标系.
∵PQ∥面ABCD,点Q在面ABCD上的射影Q′落在AB的延长线上,且PQ=1,PB=$\sqrt{2}$,
连接OQ′,则四边形POQ′Q为矩形,则OQ′=PQ=1,
又OB=1,且∠OBQ′=60°,得△OBQ′为正三角形,则BQ′=1.
∵PB=$\sqrt{2}$,∴OP=1.
∴B(-1,0,0),P(0,0,1),Q($-\frac{1}{2}$,-$\frac{\sqrt{3}}{2}$,1),D(0,$\sqrt{3}$,0),A(-2,$\sqrt{3}$,0).
$\overrightarrow{PB}=(-1,0,-1)$,$\overrightarrow{PQ}=(-\frac{1}{2},-\frac{\sqrt{3}}{2},0)$,$\overrightarrow{PA}=(-2,\sqrt{3},-1)$,$\overrightarrow{AD}=(2,0,0)$.
设平面PBQ的一个法向量为$\overrightarrow{m}=({x}_{1},{y}_{1},{z}_{1})$,
由$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{PB}=0}\\{\overrightarrow{m}•\overrightarrow{PQ}=0}\end{array}\right.$,得$\left\{\begin{array}{l}{-{x}_{1}-{z}_{1}=0}\\{-\frac{1}{2}{x}_{1}-\frac{\sqrt{3}}{2}{y}_{1}=0}\end{array}\right.$,取${y}_{1}=-\sqrt{3}$,得$\overrightarrow{m}=(3,-\sqrt{3},-3)$;
设平面PAD的一个法向量为$\overrightarrow{n}=({x}_{2},{y}_{2},{z}_{2})$,
由$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{PA}=0}\\{\overrightarrow{n}•\overrightarrow{AD}=0}\end{array}\right.$,得$\left\{\begin{array}{l}{-2{x}_{2}+\sqrt{3}{y}_{2}-{z}_{2}=0}\\{2{x}_{2}=0}\end{array}\right.$,取${y}_{2}=\sqrt{3}$,得$\overrightarrow{n}=(0,\sqrt{3},3)$.
∴cos<$\overrightarrow{m},\overrightarrow{n}$>=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}||\overrightarrow{n}|}$=$\frac{-12}{\sqrt{21}×2\sqrt{3}}=-\frac{2\sqrt{7}}{7}$.
∴平面PBQ与平面PAD所成钝二面角的余弦值为$-\frac{2\sqrt{7}}{7}$,则正弦值为$\frac{\sqrt{21}}{7}$,
正切值为$\frac{\frac{\sqrt{21}}{7}}{-\frac{2\sqrt{7}}{7}}=-\frac{\sqrt{3}}{2}$.
点评 本题考查面面垂直的判定,考查空间想象能力和思维能力,训练了利用空间向量求二面角的大小,是中档题.

| A. | 数列{An}是等差数列,数列{Bn}是等比数列 | |
| B. | 数列{An}与{Bn}都是等差数列 | |
| C. | 数列{An}是等比数列,数列{Bn}是等差数列 | |
| D. | 数列{An}与{Bn}都是等比数列 |
| A. | (-$\frac{1}{60}$,0) | B. | (0,$\frac{15}{4}$) | C. | (0,-$\frac{15}{4}$) | D. | ($\frac{1}{60}$,0) |
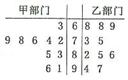 渝州集团对所有员工进行了职业技能测试从甲、乙两部门中各任选10名员工的测试成绩(单位:分)数据的茎叶图如图所示.
渝州集团对所有员工进行了职业技能测试从甲、乙两部门中各任选10名员工的测试成绩(单位:分)数据的茎叶图如图所示.