题目内容

在锐角三角形中，a、b、c分别是内角A、B、C的对边，设B=2A，则
b
a
的取值范围是（　　）
A、（-2，2）
B、（0，2）
C、（
2
，2）
D、（
2
，
3
）
考点：正弦定理,二倍角的余弦
专题：解三角形
分析：利用倍角公式和正弦定理可得
b
a
=
sinB
sinA
=2cosA．再利用B=2A及锐角三角形、cosA的单调性即可得出．
解答： 解：∵B=2A，
∴sinB=sin2A=2sinAcosA，
∴
sinB
sinA
=2cosA，
∴由正弦定理得：
b
a
=
sinB
sinA
=2cosA，
∵锐角△ABC，
∴
π
2
＜B+A=3A＜π，
∴
π
6
＜A＜
π
4
，
∴
2
2
＜cosA＜
3
2
．
∴
2
＜2cosA＜
3
，
∴
b
a
的取值范围是（
2
，
3
）．
故选：D．
点评：此题考查了正弦定理，以及余弦函数的性质，熟练掌握正弦定理是解本题的关键．
练习册系列答案
相关题目
△ABC中acosA=bcosB时，三角形的形状是（　　）
A、正三角形
B、等腰三角形
C、等腰直角三角形
D、前面说法都错
已知函数f（x）是定义在R上的奇函数，且满足f（x+2）=f（x）．若当x∈[0，1）时，f（x）=2x-
2
，则f(log
1
2
4
2
)的值为（　　）
A、0
B、1
C、
2
D、-
2
当x≠0时，有不等式（　　）
A、ex＜1+x
B、当x＞0时，ex＜1+x；当x＜0时，ex＞1+x
C、ex＞1+x
D、当x＜0时，ex＜1+x；当x＞0时，ex＜1+x
已知椭圆两条准线间的距离是焦距的2倍，则其离心率为（　　）
A、
3
2
B、
2
2
C、6
D、2
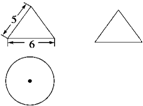有一个几何体的三视图及其尺寸如图所示（单位：cm），则该几何体的表面积及体积为（　　）
A、24π cm2，12π cm3
B、15π cm2，12π cm3
C、24π cm2，36π cm3
D、以上都不正确
下边程序运行后，打印输出的结果是（　　）
A、-5和-6B、1和-8
C、-8和-5D、1和-6
等比数列{an}各项为正数，且a2a4+a4a6+2a3a5=9，则a3+a5的值为（　　）
A、3B、6C、9D、12
已知数列{an}满足a1=
3
2
，an=2-
1
an-1
（n≥2），Sn是数列{bn}的前n项和，且有
Sn
2
=1+
n-1
n
bn．
（1）证明：数列{
1
an-1
}为等差数列；
（2）求数列{bn}的通项公式；
（3）设cn=
an
bn
，记数列{cn}的前n项和Tn，求证：Tn＜1．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网