题目内容
已知抛物线C:y2=2px(p>0)上的一点M(3,y0)到焦点F的距离等于4.
(Ⅰ)求抛物线C的方程;
(Ⅱ)若过点(4,0)的直线l与抛物线C相交于A,B两点,求△ABO面积的最小值.
(Ⅰ)求抛物线C的方程;
(Ⅱ)若过点(4,0)的直线l与抛物线C相交于A,B两点,求△ABO面积的最小值.
考点:直线与圆锥曲线的关系,抛物线的简单性质
专题:综合题,圆锥曲线的定义、性质与方程
分析:(Ⅰ)利用抛物线C:y2=2px(p>0)上的一点M(3,y0)到焦点F的距离等于4,求出p的值,可得抛物线C的方程;
(Ⅱ)解法1:分类讨论,设出直线l:y=k(x-4),与抛物线方程联立,利用韦达定理,结合面积公式,即可求△ABO面积的最小值;
解法2:设直线l:x=ty+4,与抛物线方程联立,利用韦达定理,结合面积公式,即可求△ABO面积的最小值;
(Ⅱ)解法1:分类讨论,设出直线l:y=k(x-4),与抛物线方程联立,利用韦达定理,结合面积公式,即可求△ABO面积的最小值;
解法2:设直线l:x=ty+4,与抛物线方程联立,利用韦达定理,结合面积公式,即可求△ABO面积的最小值;
解答:
解:(Ⅰ)依题意可知|MF|=3+
=4,∴p=2.故抛物线C的方程为:y2=4x.…(5分)
(Ⅱ)解法1:设A(x1,y1),B(x2,y2)
①当直线l的斜率不存在时,直线l的方程为x=4,
联立方程组
,解得y1=-4,y2=4S△ABC=
×4×|y1-y2|=16.…(8分)
②当直线l的斜率存在时,设直线l:y=k(x-4)(k≠0).
联立方程组
,消去x得y2-
y-16=0,
∴y1+y2=
,y1•y2=-16…(11分)S△ABC=
×4×|y1-y2|=2
=2
=8
>16
综合①②可得当直线l的斜率不存在时,S△ABC取得最小值16.…(13分)
解法2:设直线l:x=ty+4.
设A(x1,y1),B(x2,y2)…(7分)
联立方程组
,消去x得y2-4ty-16=0,
∴y1+y2=4t,y1•y2=-16…(10分)S△ABC=
×4×|y1-y2|=2
=2
=8
当t=0时,S△ABC取得最小值16.…(13分)
| p |
| 2 |
(Ⅱ)解法1:设A(x1,y1),B(x2,y2)
①当直线l的斜率不存在时,直线l的方程为x=4,
联立方程组
|
| 1 |
| 2 |
②当直线l的斜率存在时,设直线l:y=k(x-4)(k≠0).
联立方程组
|
| 4 |
| k |
∴y1+y2=
| 4 |
| k |
| 1 |
| 2 |
| (y1+y2)2-4y1•y2 |
16(
|
|
综合①②可得当直线l的斜率不存在时,S△ABC取得最小值16.…(13分)
解法2:设直线l:x=ty+4.
设A(x1,y1),B(x2,y2)…(7分)
联立方程组
|
∴y1+y2=4t,y1•y2=-16…(10分)S△ABC=
| 1 |
| 2 |
| (y1+y2)2-4y1•y2 |
| 16(t2+4) |
| t2+4 |
当t=0时,S△ABC取得最小值16.…(13分)
点评:本题考查抛物线的方程,考查直线与抛物线的位置关系,考查韦达定理的运用,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
已知偶函数f(x)在[0,+∞)上单调递减,则f(1)和f(-10)的大小关系为( )
| A、f(1)>f(-10) |
| B、f(1)<f(-10) |
| C、f(1)=f(-10) |
| D、f(1)和f(-10)关系不定 |
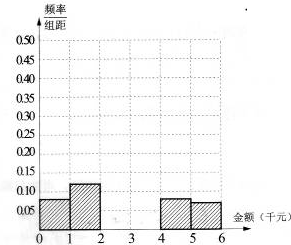 某网络营销部门随机抽查了某市200名网友在2013年11月11日的网购金额,所得数据如下表:
某网络营销部门随机抽查了某市200名网友在2013年11月11日的网购金额,所得数据如下表: