题目内容
已知函数f(x)=
,x∈[1,+∞).
(1)当a=4时,求函数f(x)的最小值;
(2)解关于x的不等式f(x)>a+3;
(3)若对任意x∈[1,+∞),f(x)>0恒成立,试求实数a的取值范围.
| x2+2x+a |
| x |
(1)当a=4时,求函数f(x)的最小值;
(2)解关于x的不等式f(x)>a+3;
(3)若对任意x∈[1,+∞),f(x)>0恒成立,试求实数a的取值范围.
考点:函数恒成立问题,函数的最值及其几何意义
专题:函数的性质及应用
分析:(1)当a=4时,利用基本不等式即可求函数f(x)的最小值;
(2)根据一元二次不等式的解法即可解关于x的不等式f(x)>a+3;
(3)若对任意x∈[1,+∞),f(x)>0恒成立,利用参数分离,然后求函数的最值,即可求实数a的取值范围.
(2)根据一元二次不等式的解法即可解关于x的不等式f(x)>a+3;
(3)若对任意x∈[1,+∞),f(x)>0恒成立,利用参数分离,然后求函数的最值,即可求实数a的取值范围.
解答:
解:(1)∵a=4,
∴f(x)=
=x+
+2≥6,
当x=2时,取得等号,
∴当x=2时,f(x)min=6.
(2)由题意得
>a+3,x∈[1,+∞),
∴x2+2x+a>(a+3)x,
∴x2-(a+1)x+a>0,
∴(x-1)(x-a)>0,
当a≤1,不等式的解为x>1,即不等式的解集为(1,+∞),
当a>1,不等式的解为x>a,即不等式的解集为(a,+∞).
(3)x∈[1,+∞),
>0恒成立,即x∈[1,+∞),x2+2x+a>0恒成立,
等价于a>-x2-2x,当x∈[1,+∞)时恒成立,
令g(x)=-x2-2x,
则当x∈[1,+∞)时,g(x)的最大值为g(1)=-1-2=-3,
∴a>-3.
∴f(x)=
| x2+2x+4 |
| x |
| 4 |
| x |
当x=2时,取得等号,
∴当x=2时,f(x)min=6.
(2)由题意得
| x2+2x+a |
| x |
∴x2+2x+a>(a+3)x,
∴x2-(a+1)x+a>0,
∴(x-1)(x-a)>0,
当a≤1,不等式的解为x>1,即不等式的解集为(1,+∞),
当a>1,不等式的解为x>a,即不等式的解集为(a,+∞).
(3)x∈[1,+∞),
| x2+2x+a |
| x |
等价于a>-x2-2x,当x∈[1,+∞)时恒成立,
令g(x)=-x2-2x,
则当x∈[1,+∞)时,g(x)的最大值为g(1)=-1-2=-3,
∴a>-3.
点评:本题主要考查不等式恒成立问题,利用参数分离法是解决此类问题的基本方法.

练习册系列答案
相关题目
 如图所示的几何体中,AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=2AB,CE与平面ACD所成角为45°,F、H分别为CD、DE中点.
如图所示的几何体中,AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=2AB,CE与平面ACD所成角为45°,F、H分别为CD、DE中点.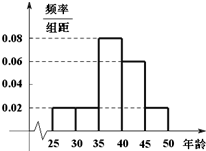 某单位N名员工参加“社区低碳你我他”活动.他们的年龄在25岁至50岁之间.按年龄分组:第1组[25,30),第2组[30,35),第3组[35,40),第4组[40,45),第5组[45,50],得到的频率分布直方图如图所示.下表是年龄的频率分布表.
某单位N名员工参加“社区低碳你我他”活动.他们的年龄在25岁至50岁之间.按年龄分组:第1组[25,30),第2组[30,35),第3组[35,40),第4组[40,45),第5组[45,50],得到的频率分布直方图如图所示.下表是年龄的频率分布表.