题目内容
在△ABC中，内角A、B、C的对边分别为a、b、c．已知bcosA-2ccosB=2bcosC-acosB．
（1）求
的值；
（2）若cosB=
，b=2，△ABC的面积S．
（1）求
| sinC |
| sinA |
（2）若cosB=
| 1 |
| 4 |
考点：余弦定理的应用,正弦定理的应用
专题：综合题,解三角形
分析：（1）利用正弦定理，结合和角的正弦公式，即可求
的值；
（2）先求出c=2a，再结合cosB=
，b=2，利用余弦定理，可求a，c的值，即可求出△ABC的面积S．
| sinC |
| sinA |
（2）先求出c=2a，再结合cosB=
| 1 |
| 4 |
解答：
解：（1）∵bcosA-2ccosB=2bcosC-acosB，
∴sinBcosA-2sinCcosB=2sinBcosC-sinAcosB，
∴sinBcosA+sinAcosB=2（sinCcosB+sinBcosC），
∴sin（A+B）=2sin（B+C），
又A+B+C=π，
∴sinC=2sinA，
∴
=2；
（2）由
=2得c=2a，
∵cosB=
，b=2，
∴由余弦定理可得4=a2+4a2-4a2×
∴解得a=1．
因此c=2，
∵cosB=
，
∴sinB=
，
∴△ABC的面积S=
acsinB=
×1×2×
=
．
∴sinBcosA-2sinCcosB=2sinBcosC-sinAcosB，
∴sinBcosA+sinAcosB=2（sinCcosB+sinBcosC），
∴sin（A+B）=2sin（B+C），
又A+B+C=π，
∴sinC=2sinA，
∴
| sinC |
| sinA |
（2）由
| sinC |
| sinA |
∵cosB=
| 1 |
| 4 |
∴由余弦定理可得4=a2+4a2-4a2×
| 1 |
| 4 |
∴解得a=1．
因此c=2，
∵cosB=
| 1 |
| 4 |
∴sinB=
| ||
| 4 |
∴△ABC的面积S=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 4 |
| ||
| 4 |
点评：本题考查正弦定理、余弦定理，和角的正弦公式，考查三角形面积的计算，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
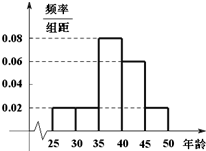某单位N名员工参加“社区低碳你我他”活动．他们的年龄在25岁至50岁之间．按年龄分组：第1组[25，30），第2组[30，35），第3组[35，40），第4组[40，45），第5组[45，50]，得到的频率分布直方图如图所示．下表是年龄的频率分布表．
参加市数学调研抽测的某校高三学生成绩分析的茎叶图和频率分布直方图均受到不同程度的破坏，但可见部分信息如下，据此解答如下问题：