题目内容
如图，把圆周长为1的圆的圆心C放在y轴上，顶点A（0，1），一动点M从A开始逆时针绕圆运动一周，记 |
| AM |
A、 |
B、 |
C、 |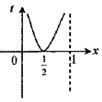
D、 |
考点：函数的图象
专题：函数的性质及应用
分析：根据动点移动过程的规律，利用单调性进行排除即可得到结论．
解答：
解：当x由0→
时，t从-∞→0，且单调递增，
由
→1时，t从0→+∞，且单调递增，
∴排除A，B，C，
故选：D．
| 1 |
| 2 |
由
| 1 |
| 2 |
∴排除A，B，C，
故选：D．
点评：本题主要考查函数图象的识别和判断，利用特殊值法，结合点的移动规律是解决本题的关键，综合性较强，有一点的难度．
练习册系列答案
阅读快车系列答案
相关题目
某几何体的三视图如图所示，其侧视图是一个边长为1的等边三角形，俯视图是两个正三角形拼成，则该几何体的体积为（ ）| A、1 | ||
B、
| ||
C、
| ||
D、
|
已知i为虚数单位，则复数
等于（ ）
| 2-i |
| 3+i |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
已知双曲线
-
=1（a，b＞0）抛物线y2=4x共焦点，双曲线与抛物线的一公共点到抛物线准线的距离为2，双曲线的离心率为e，则2e-b2的值是（ ）
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||
B、2
| ||
C、4-2
| ||
| D、4 |
已知圆C：x2+y2-4x=0，直线l：x+my-3=0，则（ ）
| A、l与C相交 |
| B、l与C相切 |
| C、l与C相离 |
| D、以上三个选项均有可能 |
命题“存在x∈R，使得x2+sinx-1≥0”的否定为（ ）
| A、对任意的x∈R，x2+sinx-1≥0 |
| B、不存在x∈R，使得x2+sinx-1≤0 |
| C、存在x∈R，使得x2+sinx-1＜0 |
| D、对任意的x∈R，使得x2+sinx-1＜0 |
已知函数f（x）=sin（2x+
），将其图象向右平移
，则所得图象的一条对称轴是（ ）
| π |
| 6 |
| π |
| 6 |
A、x=
| ||
B、x=
| ||
C、x=
| ||
D、x=
|