题目内容
已知矩阵A=
的一个特征值为λ=2,它对应的一个特征向量为
=
.
(1)求m与n的值;
(2)求A-1.
|
| α |
|
(1)求m与n的值;
(2)求A-1.
考点:特征值与特征向量的计算,逆变换与逆矩阵
专题:选作题,矩阵和变换
分析:(1)根据特征值、特征向量的定义的定义,建立方程,利用矩阵的乘法法则化简求出m与n的值;
(2)利用待定系数法求A-1.
(2)利用待定系数法求A-1.
解答:
解:(1)由题知:
=2
即
,所以m=2,n=0;
(2)由(1)知A=
,
设A-1=
,则
=
,
所以
,
所以a=
,b=0,c=-1,d=
,
所以A-1=
.
|
|
|
即
|
(2)由(1)知A=
|
设A-1=
|
|
|
|
所以
|
所以a=
| 1 |
| 2 |
| 1 |
| 2 |
所以A-1=
|
点评:本题考查待定系数法求矩阵,考查特征值与特征向量,理解特征值、特征向量的定义是关键.

练习册系列答案
相关题目
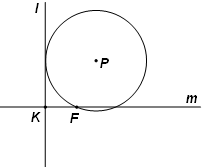 如图,已知定点F及定直线l,直线m经过F与l垂直,垂足为K,|FK|=p(p>0),动圆P经过F与l相切.
如图,已知定点F及定直线l,直线m经过F与l垂直,垂足为K,|FK|=p(p>0),动圆P经过F与l相切.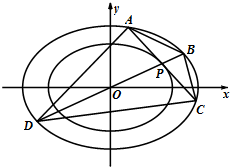 已知曲线C1:
已知曲线C1: