题目内容
 已知曲线C1:
已知曲线C1:| x2 |
| 4 |
| y2 |
| 4λ |
| x2 |
| 4λ |
| y2 |
| 4λ2 |
(Ⅰ)求λ的值;
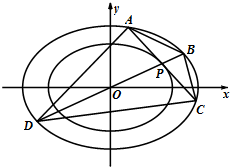
(Ⅱ)设P(x0,y0)为曲线C2上一点,过点P作直线交曲线C1于A,C两点.直线OP交曲线C1于B,D两点.若P为AC中点.
①求证:直线AC的方程为x0x+2y0y=2;
②求四边形ABCD的面积.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)由已知条件推导出
=
,由此能求出λ=
.
(Ⅱ)①由已知条件推导出x02+2y02=2,直线OP:y=
x,联立
,得B(
x0,
y0),D(-
x0,-
y0),由此能证明直线AC的方程为x0x+2y0y=2.
②联立方程组
,得2x2-4x0x+4-8
=0,由此能求出四边形ABCD的面积为4.
| 4λ |
| 4-4λ |
| 1 |
| 2 |
(Ⅱ)①由已知条件推导出x02+2y02=2,直线OP:y=
| y0 |
| x0 |
|
| 2 |
| 2 |
| 2 |
| 2 |
②联立方程组
|
| y | 2 0 |
解答:
(本题满分15分)
(Ⅰ)解:∵曲线C1:
+
=1,曲线C2:
+
=1(0<λ<1),
曲线C2的左顶点恰为曲线C1的左焦点,
∴
=
,
解得λ=
(5分)
(Ⅱ)①证明:∵λ=
,∴C1:
+
=1,C2:
+y2=1,
∵P(x0,y0)为曲线C2上一点,
过点P作直线交曲线C1于A,C两点.直线OP交曲线C1于B,D两点.
∴x02+2y02=2,直线OP:y=
x,
联立
,得B(
x0,
y0),D(-
x0,-
y0)(7分)
由kOP•kAC=-
=-
AC:y-y0=k(x-x0)=-
(x-x0),
即x0x+2y0y=2,
y0=0,x0=±
,lAC:x=±
,
符合x0x+2y0y=2,
∴直线AC的方程为x0x+2y0y=2.(9分)
②解:联立方程组
,
得(1+
)x2-
x+
-4=0,
即2x2-4x0x+4-8
=0(11分)
∴|AC|=
|xA-xC|
=
=
,
∵B,D到AC距离d1=
,d2=
(13分)
∴S=
|AC|•(d1+d2)=4,(14分)
当y0=0时,ABCD面积也为4.
综上:四边形ABCD的面积为4.(15分)
(Ⅰ)解:∵曲线C1:
| x2 |
| 4 |
| y2 |
| 4λ |
| x2 |
| 4λ |
| y2 |
| 4λ2 |
曲线C2的左顶点恰为曲线C1的左焦点,
∴
| 4λ |
| 4-4λ |
解得λ=
| 1 |
| 2 |
(Ⅱ)①证明:∵λ=
| 1 |
| 2 |
| x2 |
| 4 |
| y2 |
| 2 |
| x2 |
| 2 |
∵P(x0,y0)为曲线C2上一点,
过点P作直线交曲线C1于A,C两点.直线OP交曲线C1于B,D两点.
∴x02+2y02=2,直线OP:y=
| y0 |
| x0 |
联立
|
| 2 |
| 2 |
| 2 |
| 2 |
由kOP•kAC=-
| b2 |
| a2 |
| 1 |
| 2 |
| x0 |
| 2y0 |
即x0x+2y0y=2,
y0=0,x0=±
| 2 |
| 2 |
符合x0x+2y0y=2,
∴直线AC的方程为x0x+2y0y=2.(9分)
②解:联立方程组
|
得(1+
| ||
2
|
| 2x0 | ||
|
| 2 | ||
|
即2x2-4x0x+4-8
| y | 2 0 |
∴|AC|=
1+
|
=
1+
|
4
|
=
1+
|
8
|
∵B,D到AC距离d1=
2
| ||||||
|
2
| ||||||
|
∴S=
| 1 |
| 2 |
当y0=0时,ABCD面积也为4.
综上:四边形ABCD的面积为4.(15分)
点评:本题考查实数值的求法,考查直线方程的证明,考查四边形面积的求法,解题时要认真审题,注意点到直线的距离公式的合理运用.

练习册系列答案
相关题目