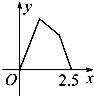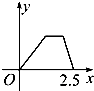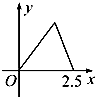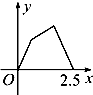题目内容
设f(x)是周期为2的奇函数,当0≤x≤1时,f(x)=2x(1-x),则f(-
)= .
| 17 |
| 4 |
考点:函数奇偶性的性质,函数的值
专题:函数的性质及应用
分析:由题意得 f(-
)=-f(
)=-f(4+
)=-f(
),代入已知条件进行运算.
| 17 |
| 4 |
| 17 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
解答:
解:∵f(x)是周期为2的奇函数,当0≤x≤1时,f(x)=2x(1-x),
f(-
)=-f(
)=-f(4+
)=-f(
)=-2×
×(1-
)=-
.
故答案为:-
f(-
| 17 |
| 4 |
| 17 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 3 |
| 8 |
故答案为:-
| 3 |
| 8 |
点评:本题考查函数的周期性和奇偶性的应用,以及求函数的值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知函数f(x+1)的定义域为[1,2],则函数y=f(
)的定义域为( )
| x+1 |
| A、[1,2] |
| B、[2,4] |
| C、[3,8] |
| D、[5,10] |
 在空间四边形S-ABC中,SA=SB=SC,三角形ABC为等边三角形,M,N分别是AB,SC的中点.
在空间四边形S-ABC中,SA=SB=SC,三角形ABC为等边三角形,M,N分别是AB,SC的中点.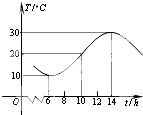 如图,某地一天从6~14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+b.
如图,某地一天从6~14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+b.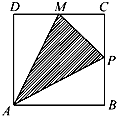 如图甲所示,点P在边长为1的正方形的边上运动,设M是CD边的中点,则当点P沿着A-B-C-M运动时,以点P经过的路程x为自变量,三角形APM的面积函数的图象形状大致是图乙中的( )
如图甲所示,点P在边长为1的正方形的边上运动,设M是CD边的中点,则当点P沿着A-B-C-M运动时,以点P经过的路程x为自变量,三角形APM的面积函数的图象形状大致是图乙中的( )