题目内容
 在空间四边形S-ABC中,SA=SB=SC,三角形ABC为等边三角形,M,N分别是AB,SC的中点.
在空间四边形S-ABC中,SA=SB=SC,三角形ABC为等边三角形,M,N分别是AB,SC的中点.(1)求SM与BN的所成角;
(2)连接CM,过N作SM的 平行线NQ,交CM与Q,连接BQ,求∠BNQ.
考点:异面直线及其所成的角
专题:空间角
分析:(1)连接CM,过N作NQ∥SM,并连接BQ,设SA=a,AB=b,根据中位线的性质,直角三角形边的关系以及余弦定理表示出BN,NQ,BQ,并根据余弦定理求出cos∠BNQ,从而求得∠BNQ,并根据∠BNQ的大小判断该角是否是异面直线SM,BN所成的角,并求出这个角;
(2)根据(1)便知∠BNQ.
(2)根据(1)便知∠BNQ.
解答:
解:(1)如图,连接CM,过N作SM的平行线NQ,交CM与Q,连接BQ;
∵设SA=a,AB=b,则SM=
,NQ2=
a2-
b2;
BQ2=
(b2-
b2)+
b2=
b2;
cos∠BSC=
,∴BN2=a2-
a2-a2•
=
b2-
a2;
∴cos∠BNQ=
=
=0;
∴∠BNQ=90°;
∵NQ∥SM,∴∠BNQ是异面直线SM与BN的所成角,即所成的角为90°;
(2)由(1)知∠BNQ=90°.
∵设SA=a,AB=b,则SM=
a2-
|
| 1 |
| 4 |
| 1 |
| 16 |
BQ2=
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 7 |
| 16 |
cos∠BSC=
| 2a2-b2 |
| 2a2 |
| 1 |
| 4 |
| 2a2-b2 |
| 2a2 |
| 1 |
| 2 |
| 1 |
| 4 |
∴cos∠BNQ=
| NQ2+BN2-BQ2 |
| 2NQ•BN |
| ||||||||||
| 2NQ•BN |
∴∠BNQ=90°;
∵NQ∥SM,∴∠BNQ是异面直线SM与BN的所成角,即所成的角为90°;
(2)由(1)知∠BNQ=90°.
点评:考查直角三角形边的关系,中位线的性质,余弦定理,异面直线所成的角的概念及求法.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
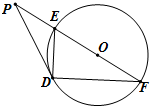 如图,P是圆O外一点,PD为切线,D为切点,割线PEF经过圆心O,若PF=12,PD=4
如图,P是圆O外一点,PD为切线,D为切点,割线PEF经过圆心O,若PF=12,PD=4