题目内容

设方阵A满足A2-A-2E=0，证明：A和A+2E均可逆，并求A和A+2E的逆矩阵．
考点：逆变换与逆矩阵
专题：矩阵和变换
分析：由已知可得A×
A-E
2
=E，即所以A可逆，逆矩阵为
A-E
2
，由已知可得A2=A+2E，结合A可逆知A2可逆，可得A+2E可逆，进而得到答案．
解答： 证明：∵方阵A满足A2-A-2E=0，
∴A2-A=2E，
∴A×
A-E
2
=E
所以A可逆，逆矩阵为
A-E
2
，
∵方阵A满足A2-A-2E=0，
∴A2=A+2E，
由A可逆知A2可逆，
所以A+2E可逆，
逆矩阵为[
A-E
2
]2=
(A-E)2
4
点评：本题考查逆变换与逆矩阵，本题是一个基础题，解题的关键是记住求你矩阵的方法，
练习册系列答案
相关题目
解不等式：2x2-9≤0．
两学生在学校操场完成老师布置的实习作业，已知两人从同一起点A出发，沿两个不同的方向分别以60米/分钟、100米/分钟的速度离开出发点A，5分钟后分别到达B点与C点，他们测得B、C之间的距离是700米，现在请你帮助他们计算他们离开A点向外跑开的不同方向之间的夹角为
 
．
已知
a
=（sinx，
3
2
），
b
=（cosx，-1），若
a
∥
b
，求2cos2x-sin2x的值．
已知数列{an}满足a1=
1
4
，（1-an）an+1=
1
4
．
（1）求证：数列{
1
an-
1
2
}为等差数列；
（2）求证：
a2
a1
+
a3
a2
+…+
an+1
an
＜n+
3
4
．
设f（x）是周期为2的奇函数，当0≤x≤1时，f（x）=2x（1-x），则f(-
17
4
)=
 
．
数列{an}满足an+1+（-1）nan=2n-1，则{an}的前4项和为
 
．
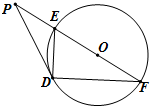如图，P是圆O外一点，PD为切线，D为切点，割线PEF经过圆心O，若PF=12，PD=4
3
，求线段DE的长度．
已知函数f（x）=a2x+2ax-1（a＞0，且a≠1）在区间[-1，1]上的最大值为14，求实数a的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网