题目内容
2．过双曲线的右焦点F作实轴所在直线的垂线，交双曲线于A，B两点，设双曲线的左顶点M，若△MAB是直角三角形，则此双曲线的离心率e的值为2．分析 由题意，△AMF为等腰直角三角形，|AF|为|AB|的一半，|AF|=$\frac{{b}^{2}}{a}$．而|MF|=a+c，由题意可得，a+c=$\frac{{b}^{2}}{a}$，即可得出结论．
解答 解：由题意，△AMF为等腰直角三角形，
|AF|为|AB|的一半，|AF|=$\frac{{b}^{2}}{a}$．
而|MF|=a+c，
由题意可得，a+c=$\frac{{b}^{2}}{a}$，
即a2+ac=b2=c2-a2，即c2-ac-2a2=0．
两边同时除以a2可得，e2-e-2=0，解之得，e=2．
故答案为：2．
点评 本题主要考查双曲线的基本性质，考查学生的计算能力，属于中档题．
练习册系列答案
相关题目
15．如果实数xy满足$\left\{\begin{array}{l}{2x+y≤2}\\{x-y≥-1}\\{x+ay≤-1}\end{array}\right.$（a＞0）．目标函数z=ax+y有最大值，则实数a的取值范围是（ ）
| A． | （$\frac{1}{2}$，1） | B． | [1，2] | C． | （1，+∞） | D． | [$\frac{1}{2}$，+∞） |
16．已知数列{an}中，a1=1，a2=2，an=an-1-an-2（n∈N*，n≥3），则a2006=（ ）
| A． | 1 | B． | -1 | C． | 2 | D． | -2 |
13．焦点在y轴上，离心率为$\frac{\sqrt{6}}{3}$，一条准线是y=3的椭圆标准方程是（ ）
| A． | $\frac{{x}^{2}}{6}$$+\frac{{y}^{2}}{2}$=1 | B． | $\frac{{x}^{2}}{4}$+y2=1 | C． | $\frac{{x}^{2}}{2}$$+\frac{{y}^{2}}{6}$=1 | D． | x2$+\frac{{y}^{2}}{4}$=1 |
20．在等差数列中，am=n，an=m（m≠n），则am+n为（ ）
| A． | m-n | B． | 0 | C． | m2 | D． | n2 |
7．某医院对治疗支气管肺炎的两种方案A，B进行比较研究，将志愿者分为两组，分别采用方案A和方案B进行治疗，统计结果如下：
（Ⅰ）完成上述列联表，并比较两种治疗方案有效的频率；
（Ⅱ）能否在犯错误的概率不超过0.05的前提下认为治疗是否有效与方案选择有关？
附：${K^2}=\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$，其中n=a+b+c+d
| 有效 | 无效 | 合计 | |
| 使用方案A组 | 96 | 120 | |
| 使用方案B组 | 72 | ||
| 合计 | 32 |
（Ⅱ）能否在犯错误的概率不超过0.05的前提下认为治疗是否有效与方案选择有关？
附：${K^2}=\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$，其中n=a+b+c+d
| P（K2≥k0） | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
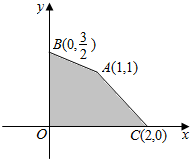给出平面区域为图中四边形ABOC内部及其边界，目标函数为z=ax-y，若当且仅当x=1，y=1时，目标函数z取最小值，则实数a的取值范围是$-1＜a＜-\frac{1}{2}$．