题目内容
9.已知k,m∈N*,若存在互不相等的正整数a1,a2,…,am,使得a1a2,a2a3,…,am-1am,ama1同时小于k,则记f(k)为满足条件的m的最大值.(1)求f(6)的值;
(2)对于给定的正整数n(n>1),
(ⅰ)当n(n+2)<k≤(n+1)(n+2)时,求f(k)的解析式;
(ⅱ)当n(n+1)<k≤n(n+2)时,求f(k)的解析式.
分析 (1)由题意,取a1=1,a2=2,a1a2<6,满足题意,若?a3≥3,则必有a2a3≥6,不满足题意,即可得出m的值.
(2)由题意,当n(n+1)<k≤(n+1)(n+2)时,设A1={1,2,…,n},A2={n+1,n+2,n+3,…},通过分析可得:f(k)≤2n,
(ⅰ)当n(n+2)<k≤(n+1)(n+2)时,取一串数ai为:1,2n,2,2n-1,3,2n-2,…,n-1,n+2,n,n+1,可得f(k)=2n.
(ⅱ)当n(n+1)<k≤n(n+2)时,从A1中选出的n个ai:1,2,…,n,考虑数n的两侧的空位,填入集合A2的两个数ap,aq,不妨设nap>naq,则nap≥n(n+2)≥k,与题意不符,可得:f(k)≤2n-1.
解答 解:(1)由题意,取a1=1,a2=2,a1a2<6,满足题意,
若?a3≥3,则必有a2a3≥6,不满足题意,
综上所述:m的最大值为2,即f(6)=2. …(4分)
(2)由题意,当n(n+1)<k≤(n+1)(n+2)时,
设A1={1,2,…,n},A2={n+1,n+2,n+3,…},
显然,?ai,ai+1∈A1时,满足aiai+1≤n(n-1)<n(n+1)<k,
∴从集合A1中选出的ai至多n个,?aj,aj+1∈A2时,ajaj+1≥(n+1)(n+2)≥k,
∴从集合A2中选出的aj必不相邻,
又∵从集合A1中选出的ai至多n个,
∴从集合A2中选出的aj至多n个,放置于从集合A1中选出的ai之间,
∴f(k)≤2n,…(6分)
(ⅰ)当n(n+2)<k≤(n+1)(n+2)时,
取一串数ai为:1,2n,2,2n-1,3,2n-2,…,n-1,n+2,n,n+1,
或写成${a_i}=\left\{{\begin{array}{l}{\frac{i+1}{2},i为奇数}\\{2n+1-\frac{i}{2},i为偶数}\end{array}}\right.$,(1≤i≤2n),
此时aiai+1≤n(n+2)<k,(1≤i≤2n-1),a2na1=n+1<k,满足题意,
∴f(k)=2n,…(8分)
(ⅱ)当n(n+1)<k≤n(n+2)时,
从A1中选出的n个ai:1,2,…,n,考虑数n的两侧的空位,填入集合A2的两个数ap,aq,不妨设nap>naq,则nap≥n(n+2)≥k,与题意不符,
∴f(k)≤2n-1,
取一串数ai为:1,2n-1,2,2n-2,3,2n-3,…,n-2,n+2,n-1,n+1,n
或写成${a_i}=\left\{{\begin{array}{l}{\frac{i+1}{2},i为奇数}\\{2n-\frac{i}{2},i为偶数}\end{array}}\right.$,(1≤i≤2n-1),
此时aiai+1≤n(n+1)<k,(1≤i≤2n-2),a2n-1a1=n<k,满足题意,
∴f(k)=2n-1.…(10分)
点评 本题考查了递推关系、构造法球数列的通项公式,考查了分析问题与解决问题的能力、推理能力与计算能力,属于难题.

| A. | m-n | B. | 0 | C. | m2 | D. | n2 |
| A. | $\frac{{x}^{2}}{4}$-y2=1 | B. | x2-$\frac{{y}^{2}}{4}$=1 | C. | $\frac{{x}^{2}}{5}$-$\frac{{x}^{2}}{4}$=1 | D. | 5x2-$\frac{5{y}^{2}}{4}$=1 |
| A. | 2 | B. | 3 | C. | 4-2ln2 | D. | 3-2ln2 |
| A. | [-2,0] | B. | (-∞,-2]∪[0,+∞) | C. | [0,2] | D. | (-∞,0]∪[2,+∞) |
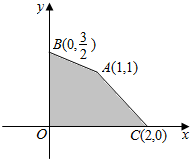 给出平面区域为图中四边形ABOC内部及其边界,目标函数为z=ax-y,若当且仅当x=1,y=1时,目标函数z取最小值,则实数a的取值范围是$-1<a<-\frac{1}{2}$.
给出平面区域为图中四边形ABOC内部及其边界,目标函数为z=ax-y,若当且仅当x=1,y=1时,目标函数z取最小值,则实数a的取值范围是$-1<a<-\frac{1}{2}$.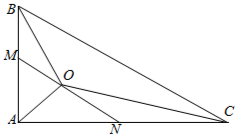 如图所示,△ABC中,AB⊥AC,AB=6,AC=8.边AB,AC的中点分别为M,N.若O为线段MN上任一点,则$\overrightarrow{OB}•\overrightarrow{OC}+\overrightarrow{OA}•\overrightarrow{OB}+\overrightarrow{OA}•\overrightarrow{OC}$的取值范围是[$-\frac{180}{11},-9$].
如图所示,△ABC中,AB⊥AC,AB=6,AC=8.边AB,AC的中点分别为M,N.若O为线段MN上任一点,则$\overrightarrow{OB}•\overrightarrow{OC}+\overrightarrow{OA}•\overrightarrow{OB}+\overrightarrow{OA}•\overrightarrow{OC}$的取值范围是[$-\frac{180}{11},-9$].