题目内容
已知向量
=(-1，2)，
=（3，m），m∈R，则“m=-6”是“
∥(
+
)”的（ ）
| a |
| b |
| a |
| a |
| b |
| A、充要条件 |
| B、充分不必要条件 |
| C、必要不充分条件 |
| D、既不充分也不必要条件 |
考点：平面向量共线（平行）的坐标表示
专题：平面向量及应用
分析：由
∥(
+
)?-1×（2+m）-2×2=0，即可得出．
| a |
| a |
| b |
解答：
解：
+
=（-1，2）+（3，m）=（2，2+m）．
由
∥(
+
)?-1×（2+m）-2×2=0，?m=-6．
因此“m=-6”是“
∥(
+
)”的充要条件．
故选：A．
| a |
| b |
由
| a |
| a |
| b |
因此“m=-6”是“
| a |
| a |
| b |
故选：A．
点评：本题考查了向量的共线定理、充要条件，属于基础题．
练习册系列答案
桃李文化快乐暑假武汉出版社系列答案
相关题目
已知A、B、C是单位圆上三个互不相同的点．若|
|=|
|，则
•
的最小值是（ ）
| AB |
| AC |
| AB |
| AC |
| A、0 | ||
B、-
| ||
C、-
| ||
D、-
|
一个侧棱与底面垂直的棱柱被一个平面截去一部分后所剩几何体的三视图如图所示，则截去那一部分的体积为．（ ）| A、1 | ||
B、
| ||
| C、11 | ||
| D、12 |
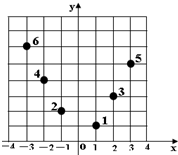如图，坐标纸上的每个单元格的边长为1，由下往上的六个点：1，2，3，4，5，6的横纵坐标分别对应数列{an}（n∈N*）的前12项，如下表所示：| a1 | a2 | a3 | a4 | a5 | a6 | a7 | a8 | a9 | a10 | a11 | a12 |
| x1 | y1 | x2 | y2 | x3 | y3 | x4 | y4 | x5 | y5 | x6 | y6 |
| A、501 | B、502 |
| C、503 | D、504 |
复数z=
的虚部为（ ）
| 2 |
| -1+i |
| A、-1 | B、-i | C、1 | D、i |