题目内容
15.已知P是△ABC内的一点(不含边界),且$\overrightarrow{AB}$•$\overrightarrow{AC}$=2$\sqrt{3}$,∠BAC=30°若△PBC,△PAB,△PCA的面积分别为x,y,z,记h(x,y,z)=$\frac{1}{x}$+$\frac{4}{y}$+$\frac{9}{z}$,则h(x,y,z)的最小值为( )| A. | 26 | B. | 32 | C. | 36 | D. | 48 |
分析 由向量的数量积公式和三角形的面积公式可得x+y+z=1,再根据基本不等式即可求出答案.
解答 解:∵$\overrightarrow{AB}$•$\overrightarrow{AC}$=2$\sqrt{3}$,∠BAC=30°,
∴|$\overrightarrow{AB}$|•|$\overrightarrow{AC}$|•cos30°=2$\sqrt{3}$,
∴|$\overrightarrow{AB}$|•|$\overrightarrow{AC}$|=4.
∵S△ABC=$\frac{1}{2}$|$\overrightarrow{AB}$|•|$\overrightarrow{AC}$|•sin30°=1=x+y+z.
∴f(x,y,z)=$\frac{1}{x}$+$\frac{4}{y}$+$\frac{9}{z}$=($\frac{1}{x}$+$\frac{4}{y}$+$\frac{9}{z}$)(x+y+z)
=1+4+9+$\frac{4x}{y}$+$\frac{y}{x}$+$\frac{9x}{z}$+$\frac{z}{x}$+$\frac{4z}{y}$+$\frac{9y}{z}$≥14+4+6+12=36,
即f(x,y,z)的最小值为36,
故选:C.
点评 本题主要考查两个向量的数量积的定义,基本不等式的应用,属于中档题.

练习册系列答案
相关题目
20.(x3+x)3(-7+$\frac{1}{{x}^{2}}$)的展开式x3中的系数为( )
| A. | 3 | B. | -4 | C. | 4 | D. | -7 |
5.假设关于某设备的使用年限x(年)和所支出的维修费用y(万元)有如表的统计资料:
若由资料可知y对x呈线性相关关系,试求:
(1)线性回归直线方程;
(2)根据回归直线方程,估计使用年限为20年时,维修费用是多少?
回归直线方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$的系数为:$\left\{\begin{array}{l}{\stackrel{∧}{b}=\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}=\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}}\\{\stackrel{∧}{b}=\overline{y}-\stackrel{∧}{b}\overline{x}}\end{array}\right.$.
| 使用年限x(年) | 2 | 3 | 4 | 5 | 6 |
| 维修费用y(万元) | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
(1)线性回归直线方程;
(2)根据回归直线方程,估计使用年限为20年时,维修费用是多少?
回归直线方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$的系数为:$\left\{\begin{array}{l}{\stackrel{∧}{b}=\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}=\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}}\\{\stackrel{∧}{b}=\overline{y}-\stackrel{∧}{b}\overline{x}}\end{array}\right.$.
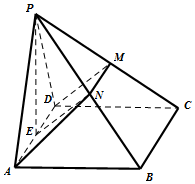 在四棱锥P-ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为2的菱形,∠BAD=60°,N是PB的中点,过A、D、N三点的平面交PC于M,E为AD中点.
在四棱锥P-ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为2的菱形,∠BAD=60°,N是PB的中点,过A、D、N三点的平面交PC于M,E为AD中点.