题目内容
如图，D为等腰三角形ABC底边AB的中点，则下列等式恒成立的是（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点：平面向量数量积的运算
专题：平面向量及应用
分析：由于D为等腰三角形ABC底边AB的中点，可得CD⊥AB，即可得出
•
=0．
| CD |
| AB |
解答：
解：∵D为等腰三角形ABC底边AB的中点，
∴CD⊥AB．
∴
•
=0．
故选：B．
∴CD⊥AB．
∴
| CD |
| AB |
故选：B．
点评：本题考查了等腰三角形的性质、向量垂直与数量积的关系，属于基础题．
练习册系列答案
应用题作业本系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
将1，2，3，4，5，6，7，8，这八个数分别填写于一个圆周的八等分点上，使得圆周上任意两个相邻位置的数之和为质数，如果圆周旋转后能重合的算作相同填法，那么不同的填法有（ ）
| A、4种 | B、8种 |
| C、12种 | D、16种 |
已知集合A={x∈R|0＜x＜1}，B={x∈R|（2x-1）（x+1）≤0}，则（∁RA）∩B（ ）
A、[0，
| ||
| B、[-1，0] | ||
C、[
| ||
| D、（-∞，-1]∪[0，+∞） |
若a=sin2，b=cos2，则a，b的大小为（ ）
| A、a＜b | B、b＜a |
| C、a=b | D、不能确定 |
如图，将无盖正方体纸盒展开，直线AB，CD在原正方体中的位置关系是（ ）| A、平行 | B、相交且垂直 |
| C、异面 | D、相交成60° |
在△ABC中，
=
，
=
，D为BC的中点，则
为（ ）
| AB |
| a |
| AC |
| b |
| AD |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
在△ABC中，|AC|2=
•
，
=（-2，-3），
=（m，1），则m的值等于（ ）
| BC |
| AC |
| BA |
| BC |
| A、8 | ||
| B、-8 | ||
C、
| ||
D、-
|
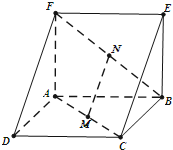如图，三棱柱ADF-BCE中，除DF、CE外，其他的棱长均为2，AB⊥AF，平面ABCD⊥平面ABEF，M，N分别是AC，BF上的中点．