题目内容
已知函数f(x)=
x3-ax+1.
(1)若x=1时,f(x)取得极值,求实数a的值;
(2)求f(x)在[0,1]上的最小值.
| 1 |
| 3 |
(1)若x=1时,f(x)取得极值,求实数a的值;
(2)求f(x)在[0,1]上的最小值.
考点:利用导数研究函数的极值,利用导数求闭区间上函数的最值
专题:导数的综合应用
分析:(1)由条件“f(x)在x=1处取得极值”可得f′(1)=0,解方程即可;
(2)先求导数f′(x),然后讨论a的值,判断f′(x)的正负,进而得到f(x)在[0,1]上的单调性,即可得到f(x)在[0,1]上的最小值.
(2)先求导数f′(x),然后讨论a的值,判断f′(x)的正负,进而得到f(x)在[0,1]上的单调性,即可得到f(x)在[0,1]上的最小值.
解答:
解:(1)f′(x)=x2-a,
因为f(x)在x=1处取得极值,所以f′(1)=0,解得a=1;
(2)f′(x)=x2-a,
①当-a≥0,即a≤0时,f′(x)=x2≥0,
则f(x)在(-∞,+∞)上为增函数,
所以f(x)在[0,1]上是增函数,
故f(x)在[0,1]上的最小值为f(0)=1;
②当-a<0,即a>0时,
由f′(x)=x2-a>0,得x<-
或x>
,所以f(x)的单调增区间为(-∞,-
)和(
,+∞);
由f′(x)=x2-a<0得-
<x<
,所以f(x)的单调减区间为(-
,
);
所以当a≥1时,f(x)在[0,1]上单调递减,
所以f(x)的最小值为f(1)=
-a;
当0<a<1时,f(x)在[0,
)上单调递减,在(
,1]上单调递增,
所以f(x)的最小值为f(
)=
(
)3-a
+1=1-
a
;
综上所述,当a≤0时,f(x)的最小值为f(0)=1;
当0<a<1时,f(x)的最小值为f(
)=
(
)3-a
+1=1-
a
;
当a≥1时,f(x)的最小值为f(1)=
-a.
因为f(x)在x=1处取得极值,所以f′(1)=0,解得a=1;
(2)f′(x)=x2-a,
①当-a≥0,即a≤0时,f′(x)=x2≥0,
则f(x)在(-∞,+∞)上为增函数,
所以f(x)在[0,1]上是增函数,
故f(x)在[0,1]上的最小值为f(0)=1;
②当-a<0,即a>0时,
由f′(x)=x2-a>0,得x<-
| a |
| a |
| a |
| a |
由f′(x)=x2-a<0得-
| a |
| a |
| a |
| a |
所以当a≥1时,f(x)在[0,1]上单调递减,
所以f(x)的最小值为f(1)=
| 4 |
| 3 |
当0<a<1时,f(x)在[0,
| a |
| a |
所以f(x)的最小值为f(
| a |
| 1 |
| 3 |
| a |
| a |
| 2 |
| 3 |
| a |
综上所述,当a≤0时,f(x)的最小值为f(0)=1;
当0<a<1时,f(x)的最小值为f(
| a |
| 1 |
| 3 |
| a |
| a |
| 2 |
| 3 |
| a |
当a≥1时,f(x)的最小值为f(1)=
| 4 |
| 3 |
点评:本题主要考查了利用导数研究函数的极值,以及利用导数研究函数的单调性和利用导数求闭区间上函数的最值,属于中档题.

练习册系列答案
相关题目
若复数m2-2m-3+(m2-3m-4)i为纯虚数(i为虚数单位),则实数m=( )
| A、m=-1 |
| B、m=3 |
| C、m=-1或 m=3 |
| D、m=0 |
若a=sin2,b=cos2,则a,b的大小为( )
| A、a<b | B、b<a |
| C、a=b | D、不能确定 |
在△ABC中,
=
,
=
,D为BC的中点,则
为( )
| AB |
| a |
| AC |
| b |
| AD |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
在△ABC中,|AC|2=
•
,
=(-2,-3),
=(m,1),则m的值等于( )
| BC |
| AC |
| BA |
| BC |
| A、8 | ||
| B、-8 | ||
C、
| ||
D、-
|
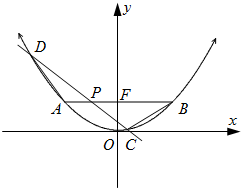 如图,已知抛物线M的参数方程为
如图,已知抛物线M的参数方程为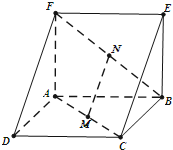 如图,三棱柱ADF-BCE中,除DF、CE外,其他的棱长均为2,AB⊥AF,平面ABCD⊥平面ABEF,M,N分别是AC,BF上的中点.
如图,三棱柱ADF-BCE中,除DF、CE外,其他的棱长均为2,AB⊥AF,平面ABCD⊥平面ABEF,M,N分别是AC,BF上的中点.