题目内容
4.设P,Q分别为圆x2+y2-8x+15=0和抛物线y2=4x上的点.则P,Q两点间的最小距离是2$\sqrt{3}$-1.分析 由题意可得圆的圆心和半径,由二次函数可得P与圆心距离的最小值,减半径即可.
解答 解:∵圆x2+y2-8x+15=0可化为(x-4)2+y2=1,
∴圆的圆心为(4,0),半径为1,
设P(x0,y0)为抛物线y2=4x上的任意一点,
∴y02=4x0,∴P与(4,0)的距离d=$\sqrt{({x}_{0}-4)^{2}+{{y}_{0}}^{2}}$=$\sqrt{({x}_{0}-2)^{2}+12}$,
∴由二次函数可知当x0=2时,d取最小值2$\sqrt{3}$,
∴所求最小值为:2$\sqrt{3}$-1.
故答案为:2$\sqrt{3}$-1.
点评 本题考查两点间的距离公式,涉及抛物线和圆的知识,属中档题.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
16.设x∈[0,3],执行如图所示的程序框图,从输出的结果中随机取一个数a,则“a≤5”的概率为( )
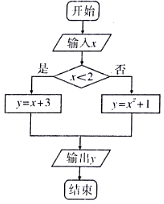

| A. | $\frac{2}{3}$ | B. | $\frac{5}{6}$ | C. | $\frac{2}{7}$ | D. | $\frac{5}{7}$ |
13.已知函数f(x)=x3+ax+1的图象在点(1,f(1))处的切线过点(2,7),则a=( )
| A. | -1 | B. | 1 | C. | 2 | D. | 3 |