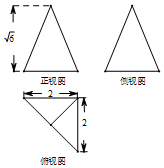
��Ŀ����
12�������ĸ����ۣ���ȷ�������ʼ�Ա�����ٴ��ݵIJ�Ʒ������ˮ���ϣ�ÿ���10���ӳ�ȡһ����Ʒ����ij��ָ���⣬�����ij����Ƿֲ������
����Ƶ�ʷֲ�ֱ��ͼ�У�����С���ε����֮����1��
���ڻع�ֱ�߷���$\stackrel{��}{y}$=0.2x+12�У�������xÿ����һ����λʱ������yһ������0.2����λ��
�ܶ��������������X��Y�������ͳ����K2�Ĺ۲�ֵk���۲�ֵkԽ��������Ϊ��X��Y�й�ϵ���İ��ճ̶Ⱦ�Խ��������
| A�� | �٢� | B�� | �ڢ� | C�� | �٢� | D�� | �ڢ� |
���� ��ϵͳ�����ͷֲ�����ĸ����жϢ٣���Ƶ�ʷֲ�ֱ��ͼ�о�������������жϢڣ��ɻع�ֱ�߷��̵�һ����ϵ���ķ��ţ������жϢۣ��ɹ۲�ֵk����������X��Y�й�ϵ�жϢܣ�
��� �⣺���ʼ�Ա�����ٴ��ݵIJ�Ʒ������ˮ���ϣ�ÿ���10���ӳ�ȡһ����Ʒ����ij��ָ���⣬�����ij�����ϵͳ�������ʢٴ���
����Ƶ�ʷֲ�ֱ��ͼ�У�����С���ε����֮����1���ʢ���ȷ��
���ڻع�ֱ�߷���$\stackrel{��}{y}$=0.2x+12�У�������xÿ����һ����λʱ������yƽ������0.2����λ���ʢ۴���
�ܶ��������������X��Y�������ͳ����K2�Ĺ۲�ֵk���۲�ֵkԽ��������Ϊ��X��Y�й�ϵ���İ��ճ̶Ⱦ�Խ�ʢ���ȷ����
����ȷ�������Ǣڢܣ�
��ѡ��D��
���� ���⿼�����������жϺ�Ӧ�ã�������������ͻع�ֱ�߷��̡���������Ĺ۲�ֵ�����ڻ����⣮

��ϰ��ϵ�д�
�����Ŀ
2����֪˫����$\frac{x^2}{3}-\frac{y^2}{2}=1$�����ҽ���ֱ�ΪF1��F2��OΪ����ԭ�㣬ԲO����F1F2Ϊֱ����Բ��ֱ��$l��\sqrt{2}x+\sqrt{3}y+t=0$��ԲO�й����㣮��ʵ��t��ȡֵ��Χ�ǣ�������
| A�� | $[{-2\sqrt{2}��2\sqrt{2}}]$ | B�� | [-4��4] | C�� | [-5��5] | D�� | $[{-5\sqrt{2}��5\sqrt{2}}]$ |