题目内容
已知函数y=f(x)是定义在R上的奇函数,对?x∈R都有f(x-1)=f(x+1)成立,当x∈(0,1]且x1≠x2时,有
<0.给出下列命题
(1)f(1)=0
(2)f(x)在[-2,2]上有5个零点
(3)点(2014,0)是函数y=f(x)的一个对称中心
(4)直线x=2014是函数y=f(x)图象的一条对称轴.
则正确的是 .
| f(x2)-f(x1) |
| x2-x1 |
(1)f(1)=0
(2)f(x)在[-2,2]上有5个零点
(3)点(2014,0)是函数y=f(x)的一个对称中心
(4)直线x=2014是函数y=f(x)图象的一条对称轴.
则正确的是
考点:抽象函数及其应用
专题:计算题,函数的性质及应用
分析:(1)令x=0,求f(1);
(2)由题意可得f(0)=f(1)=f(-1)=f(2)=f(-2)=0;
(3)证明f(2014+x)=-f(2014-x)即可;
(4)由于(3)正确,故(4)不正确.
(2)由题意可得f(0)=f(1)=f(-1)=f(2)=f(-2)=0;
(3)证明f(2014+x)=-f(2014-x)即可;
(4)由于(3)正确,故(4)不正确.
解答:
解:(1)由题意,令x=0,则f(-1)=f(1),即-f(1)=f(1),则f(1)=0;
(2)由题意,f(0)=0,f(1)=f(-1)=0,f(2)=f(1-1)=f(0)=0,f(-2)=0,
则f(x)在[-2,2]上有5个零点;
(3)由f(x-1)=f(x+1)可知,f(x)以2为周期,
∵f(2014+x)=f(x),f(2014-x)=f(-x)=-f(x),
∴f(2014+x)=-f(2014-x),
∴点(2014,0)是函数y=f(x)的一个对称中心,
(4)由于(3)正确,故(4)不正确;
故答案为:(1)(2)(3).
(2)由题意,f(0)=0,f(1)=f(-1)=0,f(2)=f(1-1)=f(0)=0,f(-2)=0,
则f(x)在[-2,2]上有5个零点;
(3)由f(x-1)=f(x+1)可知,f(x)以2为周期,
∵f(2014+x)=f(x),f(2014-x)=f(-x)=-f(x),
∴f(2014+x)=-f(2014-x),
∴点(2014,0)是函数y=f(x)的一个对称中心,
(4)由于(3)正确,故(4)不正确;
故答案为:(1)(2)(3).
点评:本题考查了函数的奇偶性的应用,属于中档题.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
已知x,y满足不等式组
,则Z=x+2y的最小值为( )
|
| A、2 | B、3 | C、4 | D、-6 |
下列四个正方体图形中,A,B为正方体的两个顶点,M,N,P分别为其所在棱的中点,则能得出AB∥平面MNP的图形个数是( )
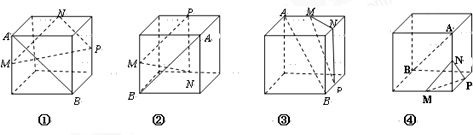

| A、1个 | B、2个 | C、3个 | D、4个 |
设正方体ABCD-A1B1C1D1的棱长为1,则平面B1AC被正方体内切球截得图形的面积( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|