Question

已知A（x₁，y₁），B（x₂，y₂）（x₁＞x₂）是函数f（x）=x³-|x|图象上的两个不同点，且在A，B两点处的切线互相平行，则

x2

x1

的取值范围为（　　）

• A、[-1，0）
• B、[-

  3

  2

  ，

  3

  2

  ]
• C、（-1，0）
• D、（-1，1）

Answer 1

考点：利用导数研究曲线上某点切线方程

专题：综合题,导数的综合应用

分析：首先把含有绝对值的函数写成分段函数的形式，然后求导，通过在A，B两点处的切线互相平行，即在A，B两点处的导数值相等，分析出A点在y轴的右侧，B点在y轴的左侧．根据A，B两点处的导数相等，得到x₁与x₂的关系式，根据关系式得出它表示的曲线，然后利用式子的几何意义求解．

解答： 解：由题意，f（x）=x³-|x|=

x3-x，x≥0 x3+x，x＜0

，
当x≥0时，f′（x）=3x²-1，当x＜0时，f′（x）=3x²+1，
因为在A，B两点处的切线互相平行，且x₁＞x₂，
所以x₁＞0，x₂＜0 （否则根据导数相等得出A、B两点重合），
所以在点A（x₁，y₁）处切线的斜率为f′（x₁）=3x₁²-1，
在点B（x₂，y₂）处切线的斜率为f′（x₂）=3x₂²+1
所以3x₁²-1=3x₂²+1，
即

x12

2 3

-

x22

2 3

=1，（x₁＞x₂，x₂＜0）
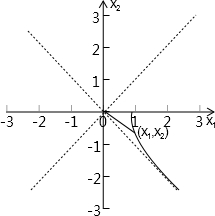
表示的曲线为双曲线在第四象限的部分，如图：

x2

x1

表示这个曲线上的点与原点连线的斜率，
由图可知

x2

x1

取值范围是（-1，0），
故选：C．

点评：本题考查了导数在研究切线方面的应用，同时考查了数形结合的思想，综合性较强，难度较大．本题的关键是把问题转化成图形的几何意义求解．