题目内容
求满足下列条件的双曲线的标准方程:
(1)渐近线方程为2x±3y=0,顶点在y轴上,且焦距为2
;
(2)与双曲线
-
=1有公共焦点,且过点(3
,2).
(1)渐近线方程为2x±3y=0,顶点在y轴上,且焦距为2
| 13 |
(2)与双曲线
| x2 |
| 16 |
| y2 |
| 4 |
| 2 |
考点:双曲线的简单性质,双曲线的标准方程
专题:圆锥曲线的定义、性质与方程
分析:(1)设出双曲线方程,利用渐近线方程为2x±3y=0,焦距为2
,列出方程组即可求解双曲线方程;
(2)利用与双曲线
-
=1有公共焦点,设出双曲线方程,利用过点(3
,2)求解即可.
| 13 |
(2)利用与双曲线
| x2 |
| 16 |
| y2 |
| 4 |
| 2 |
解答:
解:(1)设双曲线方程为
-
=1(a>0,b>0).∵c2=a2+b2,∴13=a2+b2,
由渐近线斜率得
=
,故
,解得
,
∴所求双曲线方程为
-
=1.
(2)设双曲线方程为
-
=1,将点(3
,2)代入得k=4,
所以双曲线方程为
-
=1.(通法相应给分)
| y2 |
| a2 |
| x2 |
| b2 |
由渐近线斜率得
| a |
| b |
| 2 |
| 3 |
|
|
∴所求双曲线方程为
| y2 |
| 4 |
| x2 |
| 9 |
(2)设双曲线方程为
| x2 |
| 16-k |
| y2 |
| 4+k |
| 2 |
所以双曲线方程为
| x2 |
| 12 |
| y2 |
| 8 |
点评:本题考查双曲线方程的求法,双曲线的基本性质的应用.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
对任意两实数a、b,定义运算“*”如下:a*b=
,则函数f(x)=(log
x)*log2x的值域为( )
|
| 1 |
| 2 |
| A、(-∞,0) |
| B、(0,+∞) |
| C、(-∞,0] |
| D、[0,+∞) |
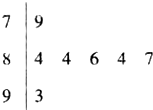 如图是2014年银川九中举行的校园之星评选活动中,七位评委为某位同学打出的分数的茎叶统计图,则数据的中位数和众数分别为( )
如图是2014年银川九中举行的校园之星评选活动中,七位评委为某位同学打出的分数的茎叶统计图,则数据的中位数和众数分别为( )| A、86,84 |
| B、84,84 |
| C、85,84 |
| D、85,93 |
(理科做) 定积分
(1-cosx)dx的值为( )
| ∫ | 2π 0 |
| A、2π | B、2π+1 |
| C、-2π | D、2π-1 |
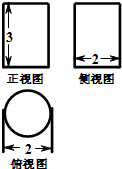 如图,一个几何体的三视图是由两个矩形和一个圆所组成,则该几何体的表面积是( )
如图,一个几何体的三视图是由两个矩形和一个圆所组成,则该几何体的表面积是( )| A、7π | B、8π |
| C、10π | D、π+12 |