题目内容
已知由长方体截去一个棱锥所得几何体的三视图如图所示,则该几何体的体积为( )


| A、16 | ||
B、
| ||
C、
| ||
D、
|
考点:由三视图求面积、体积
专题:空间位置关系与距离
分析:由已知的三视图可得:该几何体是一个长方体截去一个三棱锥得到的组合体,求出长方体和三棱锥的体积,相减可得答案.
解答:
解:利用三视图的知识可知该几何体是由一个长方体截去一个三棱锥得到,
如下图所示,

故可得几何体的体积为V=4×2×2-
×
×2×2×4=
,
故选:B.
如下图所示,

故可得几何体的体积为V=4×2×2-
| 1 |
| 3 |
| 1 |
| 2 |
| 40 |
| 3 |
故选:B.
点评:本题考查的知识点是由三视图求体积和表面积,解决本题的关键是得到该几何体的形状.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
实数x,y满足不等式
,则ω=
的取值范围是( )
|
| y+1 |
| x+1 |
A、[-1,
| ||
B、[-1,
| ||
C、(-∞,-1]∪[
| ||
D、(-∞,-1)∪(
|
已知曲线C:
-y2=1的左右焦点分别为F1F2,过点F2的直线与双曲线C的右支相交于P,Q两点,且点P的横坐标为2,则PF1Q的周长为( )
| x2 |
| 3 |
A、
| ||||
B、5
| ||||
C、
| ||||
D、4
|
已知n∈N*,数列{an}的首项a1=1,函数f(x)=
x3-(an+n+3)x2+2(2n+6)anx,若x=an+1是f(x)的极小值点,则数列{an}的通项公式为( )
| 1 |
| 3 |
A、an=
| |||||
| B、an=2n-1 | |||||
C、an=
| |||||
D、an=
|
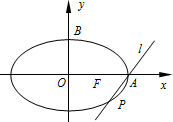 在平面直角坐标系xOy中,椭圆
在平面直角坐标系xOy中,椭圆